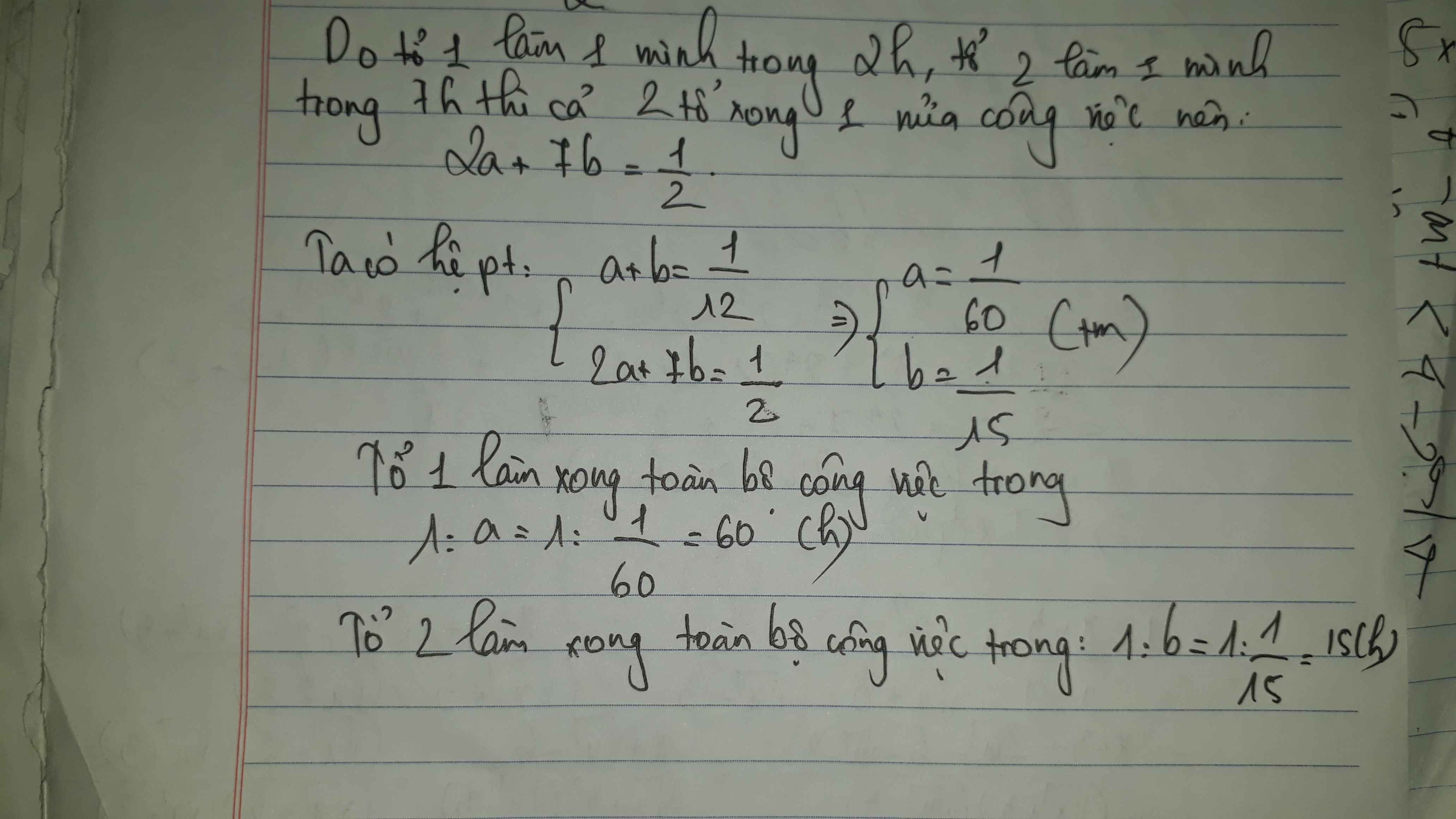Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi thời gian tổ 1 hoàn thành công việc khi làm một mình là x(giờ)
thời gian tổ 2 hoàn thành công việc khi làm một mình là y(giờ)
(Điều kiện: x>12; y>12)
Trong 1 giờ, tổ 1 làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, tổ 2 làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai tổ làm được: \(\dfrac{1}{12}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\)(1)
Vì khi tổ 1 làm một mình trong 2 giờ và tổ 2 làm một mình trong 7 giờ thi hai tổ làm được một nửa công việc nên ta có phương trình:
\(\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{6}\\\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-5}{y}=\dfrac{-1}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=15\\\dfrac{1}{x}=\dfrac{1}{12}-\dfrac{1}{15}=\dfrac{1}{60}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=60\\y=15\end{matrix}\right.\)(thỏa ĐK)
Vậy: Tổ 1 cần 60 giờ để hoàn thành công việc khi làm một mình
Tổ 2 cần 15 giờ để hoàn thành công việc khi làm một mình

Gọi thời gian tổ 1 và 2 làm một mình xong toàn bộ công việc lần lượt là a và b giờ
=> Trong 1 giờ tổ 1 làm được 1/a công việc, tổ 2 làm được 1/b công việc
Ta có: 12.1/a+12.1/b=1
và 2.1/a + 7.1/b=1/2
=> 1/a =1/60 => a =60
1/b=1/15=>b=15
Gọi thời gian tổ 1 hoàn thành công việc 1 mình là :x(h)
thòi gian tổ 2 hoàn thành công việc 1 mình là : y(h)
Một giờ tổ 1 làm được : \(\frac{1}{x}\)(công việc)
Một giờ tổ 2 làm được :\(\frac{1}{y}\)(công việc)
một giờ cả 2 làm được :\(\frac{1}{12}\)(công việc)
Ta có pt: \(\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\left(1\right)\)
Hai giờ tổ 1 làm được :\(\frac{2}{x}\)
bảy giờ tổ 2 làm được : \(\frac{7}{y}\)
Cả 2 làm được nửa công việc là :\(\frac{1}{2}\)
Ta có pt:\(\frac{2}{x}+\frac{7}{y}=\frac{1}{2}\left(2\right)\)
Từ(1) và (2) ta có hệ pt:\(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\\\frac{2}{x}+\frac{7}{x}=\frac{1}{2}\end{cases}}\)<=> \(\hept{\begin{cases}\frac{2}{x}+\frac{2}{y}=\frac{1}{6}\\\frac{2}{x}+\frac{7}{y}=\frac{1}{2}\end{cases}}\)<=>\(\hept{\begin{cases}\frac{2}{x}+\frac{2}{y}-\frac{2}{x}-\frac{7}{y}=\frac{1}{6}-\frac{1}{2}\\\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\end{cases}}\)
<=>\(\hept{\begin{cases}\frac{5}{y}=\frac{1}{3}\\\frac{1}{x}+\frac{1}{y}=\frac{1}{12}\end{cases}}\)<=>\(\hept{\begin{cases}y=15\\x=60\end{cases}}\)

Gọi thời gian tổ 1 làm một mình xong công việc là x(h); thời gian tổ 1 làm một mình xong công việc là y(h) (ĐK: x, y > 0)
Một giờ tổ 1 làm được: \(\dfrac{1}{x}\) (Công việc)
Một giờ tổ 2 làm được: \(\dfrac{1}{y}\) (Công việc)
Một giờ cả hai tổ làm được: \(\dfrac{1}{12}\) (Công việc)
Vì một giờ cả hai tổ làm được \(\dfrac{1}{12}\) công việc nên ta có pt:
\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\) (1)
Tổ 1 làm chung với tổ 2 trong 4 giờ thì phải đi làm việc khác nên tổ 1 làm được: \(\dfrac{4}{x}\) (Công việc)
Tổ 2 làm chung với tổ 1 trong 4 giờ và làm xong công việc còn lại trong 10 giờ nên tổ 2 làm được: \(\dfrac{4}{y}+\dfrac{10}{y}=\dfrac{14}{y}\) (Công việc)
Vì hai tổ làm xong 1 công việc nên ta có pt:
\(\dfrac{4}{x}+\dfrac{14}{y}=1\) (2)
Từ (1) và (2) ta có hpt:
(I) \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{4}{x}+\dfrac{14}{y}=1\end{matrix}\right.\)
Giải hpt:
(I) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{4}{y}=\dfrac{1}{3}\\\dfrac{4}{x}+\dfrac{14}{y}=1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}-\dfrac{10}{y}=\dfrac{-2}{3}\\\dfrac{4}{x}+\dfrac{14}{y}=1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}y=15\\\dfrac{4}{x}+\dfrac{14}{15}=1\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}y=15\\\dfrac{4}{x}=\dfrac{1}{15}\end{matrix}\right.\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=60\\y=15\end{matrix}\right.\) (TM)
Vậy tổ 1 làm một mình trong 60h thì xong công việc đó
tổ 2 làm một mình trong 15h thì xong công việc đó
Chúc bn học tốt!
Gọi thời gian tổ 1 làm một mình xong công việc là x(h); thời gian tổ 1 làm một mình xong công việc là y(h) (ĐK: x, y > 0)
Một giờ tổ 1 làm được: 1x1x (Công việc)
Một giờ tổ 2 làm được: 1y1y (Công việc)
Một giờ cả hai tổ làm được: 112112 (Công việc)
Vì một giờ cả hai tổ làm được 112112 công việc nên ta có pt:
1x+1y=1121x+1y=112 (1)
Tổ 1 làm chung với tổ 2 trong 4 giờ thì phải đi làm việc khác nên tổ 1 làm được: 4x4x (Công việc)
Tổ 2 làm chung với tổ 1 trong 4 giờ và làm xong công việc còn lại trong 10 giờ nên tổ 2 làm được: 4y+10y=14y4y+10y=14y (Công việc)
Vì hai tổ làm xong 1 công việc nên ta có pt:
4x+14y=14x+14y=1 (2)
Từ (1) và (2) ta có hpt:
(I) ⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩1x+1y=1124x+14

Tham khảo:
Gọi x là năng suất mà tổ (I) làm trong 1h(x>0) (công việc/h)
y là năng suất mà tổ (II) làm trong 1h (y>0) (công việc/h)
Mà tổ (I)và (II) cùng làm với nhau trong 12h thì xong 1 công việc nên ta có phương trình:
12x+12y=1 (1)
nếu 2 tổ làm trong 3h sau đó tổ II đi làm việc khác và tổ I làm thêm 7h thì được 7/12 công việc nên
10x+3y=7/12 (2)
(1),(2) ta có hệ phương trình:
12x+12y=1
10x+3y=7/12
⇒x=1/21(TM); y=1/28(TM)
Vậy Tổ (I)làm một mình trong 21h thì xong công việc.
Tổ (II) làm một mình trong 28h thì xong công việc.
Lời giải:
Giả sử tổ 1 và tổ 2 làm 1 mình thì lần lượt trong $a$ và $b$ sẽ xong công việc. ĐK: $a,b>0$.
Trong 1 giờ thì:
Tổ 1 làm được $\frac{1}{a}$ công việc
Tổ 2 làm được $\frac{1}{b}$ công việc
Ta có:
\(\left\{\begin{matrix} 12(\frac{1}{a}+\frac{1}{b})=1\\ \frac{3+7}{a}+\frac{3}{b}=\frac{7}{12}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{12}{a}+\frac{12}{b}=1\\ \frac{10}{a}+\frac{3}{b}=\frac{7}{12}\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{1}{a}=\frac{1}{21}\\ \frac{1}{b}=\frac{1}{28}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=21\\ b=28\end{matrix}\right.\) (thỏa mãn)
Vậy....

Gọi x là năng suất mà tổ (I) làm trong 1h(x>0) (công việc/h)
y là năng suất mà tổ (II) làm trong 1h (y>0) (công việc/h)
Mà tổ (I)và (II) cùng làm với nhau trong 12h thì xong 1 công việc nên ta có phương trình:
12x+12y=1 (1)
nếu 2 tổ làm trong 3h sau đó tổ II đi làm việc khác và tổ I làm thêm 7h thì được 7/12 công việc nên
10x+3y=7/12 (2)
(1),(2) ta có hệ phương trình:
12x+12y=1
10x+3y=7/12
⇒x=1/21(TM); y=1/28(TM)
Vậy Tổ (I)làm một mình trong 21h thì xong công việc.
Tổ (II) làm một mình trong 28h thì xong công việc.

Pt 1: 4(1/a + 1/b )= 1
Pt 2: 1/a + 3/b = 5/12
Từ 2 pt ta được hpt sau đó giải a,b với a là t/g người t1 làm cv đó, b là t/g người t2 làm cv đó