Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giữa M và trung trực của AB có 2 cực đại khác nên M là cực đại thứ 3 kể từ trung trực.
Vì: \(d_1-d_2=\text{k}\lambda-\frac{\lambda}{6}\)
Nên: k = 1 là cực đại thứ 1 (để cho d1 - d2 > 0).
k = 2 là cực đại thứ 2.
M là cực đại thứ 3 nên k = 3 bạn nhé.

- Từ phương trình của 2 nguồn ta thấy sóng của 2 nguồn vuông pha nhau thì số cực đại và cực tiểu là như nhau và:
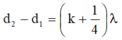
- Giữa M và đường trung trực AB còn có 2 dãy cực đại và tại M là cực tiểu → k = 2
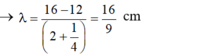
- Tốc độ truyền sóng là:
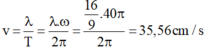

+ Từ phương trình của 2 nguồn ta thấy sóng của 2 nguồn vuông pha nhau thì số cực đại và cực tiểu là như nhau và
d 2 - d 1 = ( k + 1 4 ) λ
+ Giữa M và đường trung trực AB còn có 2 dãy cực đại và tại M là cực tiểu → k = 2
→ λ = 16 - 12 ( 2 + 1 4 ) = 16 9 cm
+ Tốc độ truyền sóng là: v = λ T = λ . ω 2 π = 16 9 . 40 π 2 π = 35 , 56 cm/s
Đáp án A

Điểm A sớm pha hơn B là: \(\frac{2}{3}\pi\)
Điểm M dao động với biên cực đại khi: \(d_2-\left(d_1-\frac{\lambda}{3}\right)=k\lambda\Rightarrow d_2-d_1=k\lambda-\frac{\lambda}{3}\)
Giả sử M lệch phía A, cách trung điểm AB là x thì:\(d_2-d_1=\frac{AB}{2}+x-\left(\frac{AB}{2}-x\right)=2x=k\lambda-\frac{\lambda}{3}\)
\(\Rightarrow x=\frac{k\lambda}{2}-\frac{\lambda}{6}\)
Nhận thấy xmin khi k = 0 \(\Rightarrow x_{min}=-\frac{\lambda}{6}\)
Dấu "-" chứng tỏ x lệch về phía ngược lại mà tả đã giả sử, là phía B.

B sớm pha hơn A nên điểm M dao động với biên độ cực đại thì:
\(\left(d_1-\frac{\lambda}{6}\right)-d_2=k\lambda\Leftrightarrow d_1-d_2=k\lambda+\frac{\lambda}{6}\)(*)
A B M d1 d2
Bước sóng: \(\lambda=2cm\)
M cách A lớn nhât thì d1 phải lớn nhất thỏa mãn (*)
\(d_1-d_2\le10\Rightarrow k\lambda+\frac{\lambda}{6}\le10\Rightarrow k.2+\frac{2}{6}\le10\Rightarrow k\le4,83\)
k nguyên \(\Rightarrow k=4\)
Ta có hệ:
\(\begin{cases}d_1-d_2=4\cdot2+\frac{2}{6}=\frac{25}{3}\\d_1+d_2=10\end{cases}\)
suy ra: \(d_1=\left(\frac{25}{3}+10\right):2=9,17cm\)

Điểm M dao động với biên độ cực đại thì: \(MA-\left(MB-\frac{\Delta\varphi}{2\pi}\lambda\right)=k\lambda\)
\(\Rightarrow MA-MB=k\lambda-\frac{\Delta\varphi}{2\pi}\lambda\)
Thay \(\Delta\varphi=-\frac{\pi}{3}\) vào biểu thức trên thì: \(\Rightarrow MA-MB=k\lambda-\frac{\lambda}{6}=\frac{\lambda}{3}\)(giả thiết)
Không tìm đc giá trị nguyên k thỏa mãn PT trên, nên \(\Delta\varphi=-\frac{\pi}{3}\) không thỏa mãn.
bạn ơi đấy là đáp án D trong ABCD
A. -pi/6 b. -2pi/3 c.2pi/3 d. -pi/3
cả A và B đều không thỏa mãn giống D mà

Đáp án A
+ Hai nguồn ngược pha nên vị trí của những điểm dao động với biên độ cực đại được xác định bởi:
![]()
Theo giả thiết, tại M ta có:
![]()
Tốc độ truyền sóng:
![]()

A B M d1 d2 B'
Mình giải thích chi tiết hơn công thức của bạn Giang Nam thế này:
B sớm pha hơn A là \(\frac{\pi}{3}\)
Mình lấy điểm B' trên phương truyền sóng BM sao cho B' cùng pha với A, nên B' trễ pha \(\frac{\pi}{3}\)so với B \(\Rightarrow BB'=\frac{\lambda}{6}\)
B' cùng pha với A nên B dao động cực đại thì: \(MB'-MA=k\lambda\Leftrightarrow\left(d_2-\frac{\lambda}{6}\right)-d_1=k\lambda\)
\(\Leftrightarrow d_2-d_1=k\lambda+\frac{\lambda}{6}\)(Trong công thức của bạn Giang Nam phải sửa lại như thế này mới đúng đc)
Dựa theo các phương án của bài toán thì d1=12cm, d2 = 18cm thỏa mãn công thức trên nên điểm M dao động biên cực đại.

Điểm B sớm pha hơn A.
Để M dao động với biên cực đại thì: \(\left(d_2-\frac{\lambda}{6}\right)-d_1=k\lambda\Rightarrow d_2-d_1=k\lambda+\frac{\lambda}{6}\)
Kể từ trung trực AB, đường cực đại thứ 1 khi k = 0
Đường thứ 2 khi k = 1
M thuộc đường thứ 3 khi k =2 \(\Rightarrow2\lambda+\frac{\lambda}{6}=24-11=13\Rightarrow\lambda=6cm\)
Vận tốc: \(v=\lambda f=6.50=300\) (cm/s)
@phynit : lần trước bạn có giải thích cho mình giả sử B' cùng pha vs A suy ra B' trễ pha hơn B là pi/3
vậy từ pi/3 ra lamđa/6 kiểu gì bạn?