Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi 12ph=0,2h
gọi vận tốc của 2 người lần lượt là v1,v2 (km/h)
Ngược chiều : S1+S2=AB
V1.t+V2.t=20
0,2V1+0,2V2=20 (1)
Cùng chiều : S1-S2=AB
V1.t/-V2.t/=AB
1V1-1V2=20 (2)
Từ (1),(2) ta có hệ pt: \(\left\{{}\begin{matrix}0,2V1+0,2V2=20\\V1-V2=20\end{matrix}\right.\)\(\Rightarrow\)\(\left\{{}\begin{matrix}V1=60\\V2=40\end{matrix}\right.\)

Ta có: 4 phút = 240 (s); 0,48km = 480m
Vì hai người đi xe đạp cùng khởi hành một lúc và chuyển động thẳng cùng chiều nên vận tốc của người thứ 1 so với người thứ 2:
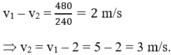
Vậy vận tốc của người thứ 2 là: 3 m/s.

bài 4:
Giải :
a.Sau khi tăng tốc thêm 3 km/h thì đến nơi sớm hơn dự kiến là 1h ,mà S là như nhau nên theo bài ra ta có:
V1.t = (V1 +3 ).(t -1).
12.t = (12+3 ).(t -1).
12.t = 15.t -15.
15 = 15.t – 12.t.
5 = t.
b. Gọi t’1 là thời gian đi quãng đường s1: t’1 = S1/V1 ( / : là chia).
Thời gian sửa xe : t = 15 phút = ¼ h.
Thời gian đi quãng đường còn lại : t’2 = (S1-S2)/V2.
Theo bài ra ta có : t1 – (t’1 + ¼ + t’2) = 30 ph = ½ h.
T1 – S1/V1 – ¼ - (S-S1)/V2 = ½. (1).
S/V1 – S/V2 – S1.(1/V1- 1/V2) = ½ +1 /4 =3/4 (2).
Từ (1) và (2) suy ra: S1.(1/V1 – 1/V2) = 1- ¾ = ¼.
Hay S1 = ¼ . (V1- V2)/(V2-V1) = ¼ . (12.15)/(15-12) = 15 km.
bài 1:
a) Lúc xe từ B xuất phat thì xxe từ A đi được quáng đường: S=40 km
*/PTCĐ:
X1= 40+ 40*t
X2= 25*t

Đổi: 0,48 km = 480 m.
Và: 4 phút = 240 giây.
\(S_1=v_1t_1=1200\left(m\right)\)
\(S_2=S_1-S=720\left(m\right)\)
\(v_2=\frac{S_2}{t_2}=\frac{720}{240}=3\) (m/s)
Đổi 5m/s= 18km/h
4 phút =\(\frac{1}{15}\left(h\right)\)
Do hai người chuyển động cùng chiều và cùng lúc
=> \(t_{gặp}=\frac{S}{v_1-v_2}=>\frac{1}{15}=\frac{0,48}{18-v_2}\)
=> \(18-v_2\)=7,2
=> \(v_2\)= 10,8 (km/h)

Chọn điểm A là vị trí xuất phát của người thứ nhất
điểm B là vị trí xuất phát của người thứ hai
điểm C là vị trí 2 ng gặp nhau
Gọi quãng đường AB, vận tốc của người thứ nhất, vận tốc của người thứ hai lần lượt là \(s_{AB},v_1,v_2\)
Thời gian 2 xe gặp nhau là t
Ta có:\(s_{AB}=0,48\left(km\right)=480\left(m\right);v_1=5\left(\dfrac{m}{s}\right);t=4'=240\left(s\right);s'=120\left(m\right)\)
a, Quãng đường từ A đến vị trí gặp nhau
\(s_{AB}+s_{BC}=s_{AC}\Rightarrow s_{AB}+v_2t=v_1t\Rightarrow480+v_2\cdot240=5\cdot240\Rightarrow v_2=3\left(\dfrac{m}{s}\right)\)
b, Thời gian người thứ nhất còn cách ng thứ hai 120m và bt là 2 ng chưa gặp nhau
ta có: \(s_1+s'=s_{AB}+s_2\Rightarrow v_1t'+s'=s_{AB}+v_2t'\Rightarrow5t'+120=480+3t'\Rightarrow t'=180\left(s\right)\)
Vậy ...
< Sửa lại cách trình bày của mình nha><Mình chỉ hướng ròi đó>

Đổi 5m/s= 18km/h
4 phút=\(\frac{2}{30}\)h
Do hai người chuyển động cùng lúc và cùng chiều nên
\(\frac{2}{30}=\frac{0,48}{v_1-v_2}=\frac{0,48}{18-v_2}\)
Giải ra ta có \(v_2\)= 10,8 (km/h)
Đổi 20 phút \(=\dfrac{1}{3}\) giờ
Nếu 2 người đi ngược chiều nhau thì tổng vận tốc của người thứ 1 và người thứ 2 là:
\(v_1+v_2=\dfrac{S}{t}=20:\dfrac{1}{3}=60\) (km/h) (1)
Nếu 2 người đi cùng chiều nhau thì ta có: \(v_1=v_2+20\Rightarrow v_1-v_2=20\) (km/h) (2)
Từ (1) và (2) \(\Rightarrow v_1=40\) km/h; \(v_2=20\) km/h
Vậy \(v_1=40\) km/h; \(v_2=20\) km/h
Đổi: 20' = \(\dfrac{1}{3}\left(h\right)\)
Tổng của hai vận tốc là:
\(t_1=\dfrac{S}{v_1+v_2}=\dfrac{20}{v_1+v_2}=\dfrac{1}{3}\Leftrightarrow v_1+v_2=60\)Hiệu của hai vận tốc là:
\(t_2=\dfrac{S}{v_1-v_2}=\dfrac{20}{v_1-v_2}=1\Leftrightarrow v_1-v_2=20\)
Vận tốc của người thứ nhất là:
\(v_1=\dfrac{\left(60+20\right)}{2}=40\left(\dfrac{km}{h}\right).\)
Vận tốc của người thứ hai là:
\(v_2=60-40=20\left(\dfrac{km}{h}\right).\)