Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số trận đấu mà anh Nam chơi ngày thứ nhất, thứ 2, ..., ngày thứ 20 lần lược là: a1; a2; ...; a n.
Xét 20 tổng :
S1 = a1
S2 = a1 + a2
...................
S n = a1 + a2 + ... + a n
Ta có: S1 < S2 < .... < S n < 36 (vì trong 20 ngày anh Nam không chơi quá 12.3 = 36 trận)
Ta biết rằng 1 số tự nhiên bất kỳ khi chia cho 20 thì có 19 số dư khác 0 là: 1, 2,...,19.
Giờ quay lại bài toán ta thấy
Nếu trong 20 tổng này có 1 tổng chia hết 20 thì bài toán đã được chứng minh (vì các tổng đó lớn hơn 0 nhỏ hơn 36 nên tổng chỉ có thể là 20).
Còn nếu trong 20 tổng này không có tổng nào chia hết cho 20 thì sẽ tồn tại ít nhất 2 tổng có cùng số dư khi chia cho 20.
Giả sử hai tổng đó là S m, S n (m > n) thì ta có S m - S n = (a1 + a2 + ... + a m) - (a1 + a2 + ... + a n) = a n+1 + a n+2 + ...+ a m chia hết cho 20. Hay S m - S n = 20.
Vậy tồn tại một số ngày liên tiếp trong đó anh chơi đúng 20 trận.

Bài này quen quá, hình như là toán lớp 5 thì phải
1/ Ta có: Trận thắng 3 điểm, trận hòa 2 điểm, trận thua 1 điểm
Số trận thắng-thua gấp đôi số trận hòa
Tổng số điểm là 176 điểm
Tỉ số điểm cho trận thắng-thua và hòa là:
(3x2) / (2x1) = 3/1
Tồng số phần bằng nhau: 3+1=4 (phần)
Số điểm cho các đội hòa là:
176 / 4 = 44 (điểm)
Số trận hòa là: 44 / 2 = 22 (trận)
Số điểm cho các đội thắng-thua là:
176 - 44 = 132 (điểm)
Số trận thắng-thua là:
132 / 3 = 44 (trận)
Tổng số các trận đấu là: 44+22 = 66 (trận)
Do n là số đội nên
n.(n-1) : 2
Ta được:
n.(n-1) : 2 = 66
n.(n-1) = 66.2 = 132
Do n và n-1 là 2 số tự nhiên liên tiếp
nên 132 = 12.11
=> n = 12
Vậy có 12 đội thi đấu

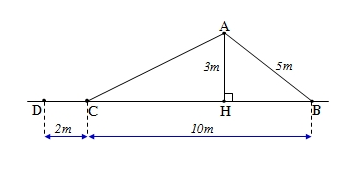
Xét tam giác vuông AHB (^AHB = 90°) ta có:
AB2 = AH2 + HB2 (vì bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông).
hay 52 = 32 + HB2
=> HB2 = 52 - 32 = 25 - 9 = 16.
HB = \(\sqrt{16}\) = 4.
Vậy HB = 4m.
Độ dài cạnh CH là:
CH = BC - HB
hay CH = 10 - 4 = 6 (m)
Vậy cạnh CH = 6m.
Xét tam giác vuông AHC (^AHC = 90°) ta có:
AC2 = AH2 + CH2
hay AC2 = 32 + 62 = 9 + 36 = 45.
AC = \(\sqrt{45}\approx7.\)
Vậy AC \(\approx7m\).
Độ dài ACD là:
ACD = AC + CD
hay ACD = 7 + 2 = 9 (m).
Vậy ACD = 9m.
2 lần BA là:
5.2 = 10 (m)
Vậy 2 lần BA = 10m.
Mà ACD < BA (9 < 10) nên đường trượt ACD ko gấp hơn hai lần đường lên BA.
Vậy bạn Mai nói sai, bạn Vân nói đúng.

Trong tam giác BCD, góc DCB là góc tù nên là góc lớn nhất. Cạnh DB đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DB > DC (1)
Vì góc DBA là góc ngoài tại đỉnh B của tam giác BCD nên \(\widehat {ABD} > \widehat {BCD}\)nên góc DBA cũng là góc tù.
Trong tam giác ABD, góc DCA là góc tù nên là góc lớn nhất. Cạnh DA đối diện với góc lớn nhất nên là cạnh lớn nhất
\( \Rightarrow \) DA > DB (2)
Từ (1) và (2) \( \Rightarrow \) DA > DB > DC
Vậy DA dài nhất, DC ngắn nhất
Do đó, cầu thủ C gần trái bóng nhất, cầu thủ A xa trái bóng nhất.

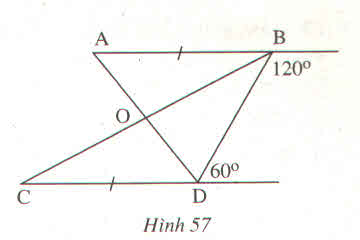
Ta có: góc B + góc D = 1200 + 600 = 1800
Mà hai góc này TCP
=> AB // CD
Xét tam giác ABO và tam giác CDO có:
AB = CD (GT)
ABC = BCD (AB // CD)
BAD = ADC (AB // CD)
=> tam giác ABO = tam giác CDO
=> AO = OD
=> O là trung điểm AD
Ta có: tam giác ABO = tam giác CDO
=> BO = OC
=> O là trung điểm BC




tham khảo:
https://olm.vn/hoi-dap/detail/1070944541422.html
Xét các số 2, 22, 222,....., 222.....222 (có p + 1 chữ số 2)
=> có p + 1 số, các số dư có thể khi chia cho p là 0 , 1, ..., p - 1 (p số dư)
=> theo ngly dirichlet thì có chắc chắn ít nhất 2 số có cùng số dư
lấy 2 số đó trừ đi nhau thì được một số chỉ gồm chữ số 2 và 0 chia hết cho p