Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+, Ta có: AC=AI+IC Mà I lại là trung điểm của AC nên ta có: AC/2=12/2=6(cm) => IA=IC=6(cm) +, Ta có: BD=DI+BI 16=DI+BI Mà I là trung điểm của AC nên ta có: BD/2=16/2=8(cm) +, Ta tam giác AID vuông tại I : =>AD 2 =AI2+ ID2(định lí Pi-Ta-Go) => AD2=62+ 82 => AD2=100 => AD=\(\sqrt{100}\) => AD=10(cm) +, Ta có tam giác AIB vuông tại I => AB 2=AI2+IB2(định lí Pi- Ta- Go) => AB2=62+82 =>AB2= 1OO =>AB=\(\sqrt{100}\) => AB=1O(cm)

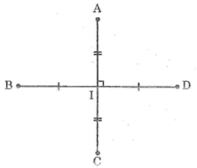
Gọi I là giao điểm của AC và BD
Ta có: I là trung điểm AC nên IA = IC = AC/2=6cm
Vì I là trung điểm của BD nên IB = ID = BD/2=8cm
Áp dụng định lí pitago vào tam giác vuông AIB ta có:
AB2=IA2+IB2
AB2=62+82=36+64=100
Vậy AB = 10 cm
Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)
Suy ra: AD = BC = CD = AB = 10cm

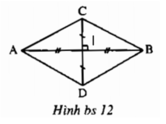
+ Gọi giao điểm của AB và CD là I. Theo giả thiết I là trung điểm của CD và AB.
+) Xét tam giác ACI và tam giác ADI có:
AI chung
CI = DI (vì I là trung điểm của CD).
∠AIC = ∠ DIA = 90º ( vì AB vuông góc với CD tại I).
Suy ra: ∆ ACI = ∆ ADI (c.g.c)
Suy ra: ∠CAI = ∠ ADI ( hai góc tương ứng).
Do đó, AB là tia phân giác của góc ∠CAD .
+) Chứng minh tương tự ta có: CD là tia phân giác của góc C, BA là tia phân giác của góc B, DC là tia phân giác của góc D.

Tự vẽ hình.
Do O là trung điểm của AB ➙OA=OB(1)
Do O là trung điểm của DC➙OC=OD(1')
Xét△ACO và △BDO có :
CO=OD(Theo 1')
Góc COA = Góc DOB =90°
AO=OB(Theo 1)
➙△ACO=△BDO (C.G.C)
➙ CA = DB ( hai cạnh tương ứng)(*)
Xét 2 tam giác vuông COB và DOA có
AO=OB (cmt)
CO=OD(cmt)
Góc AOD =góc COB =90°
➙△COB=△DOA ( c.g.c)
➙DA=CB( hai cạnh tương ứng)(**)
Xét △AOC và △BOC có
OC chung
AO=OB (cmt)
➙△AOC=△BOC(c.g.c)
➙AC=CB (***)
Từ (*)(**)(***) suy ra AC=CB=DB=AD (đpcm)
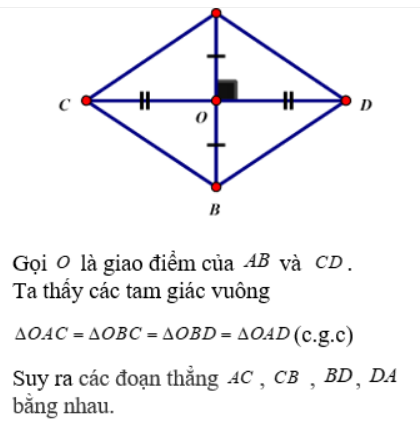



A C B D M
Gọi M là giao của AC và BD
Ta có: AC = 12 cm
M là trung điểm AC => AM = MC = 6 cm
Ta có: BD = 16 cm
M là trung điểm BD => BM = MD = 8 cm
Xét hai tam giác vuông ABM và CBM có:
BM: cạnh chung
AM = CM (cmt)
=> tam giác ABM = tam giác CBM (1)
Xét hai tam giác CBM và ADM có:
AM = MC (cmt)
BMC = AMD (đđ)
BM = MD (cmt)
=> tam giác CBM = tam giác ADM (2)
Xét hai tam giác vuông ADM và CDM có:
CM: chung
AM = MC (cmt)
=> tam giác ADM = tam giác CDM (3)
Từ (1);(2);(3)
=> bốn tam giác ABM; BCM; CAM; DAM bằng nhau
=> AB = BC = CD = DA
Ta có: tam giác ABM vuông
theo định lí pytago ta có:
AB2 = AM2 + BM2
=> AB2 = 62 + 82
=> AB2 = 100
=> AB = 10 cm
Có: AB = BC = CD = DA = 10 cm
Vậy: AB = 10 cm
BC = 10 cm
CD = 10 cm
DA = 10 cm.