Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Với giả thiết λ << L và L << d thì ta có thể coi bài toán giống như giao thoa sóng ánh sáng với:
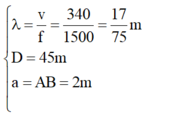
- Khoảng cách hai điểm gần nhau nhất mà nghe thấy âm nhỏ nhất tương ứng với 1 khoảng vân nên:
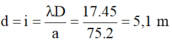

+ Với giả thiết l << L và L << d thì ta có thể coi bài toán giống như giao thoa sóng ánh sáng với:
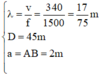
+ Khoảng cách hai điểm gần nhau nhất mà nghe thấy âm nhỏ nhất tương ứng với 1 khoảng vân nên:
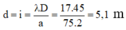
Đáp án C

Đáp án D
![]()
Độ lệch pha giữa M và O:
![]() ;
;
điểm dao động với biên độ cực tiểu trên AB thỏa mãn ![]()
Điểm N dao động với biên độ cực tiểu và gần A nhất suy ra:
![]() = 7,5
= 7,5
Suy ra:

N q1 q2 A E1 E2
Ta có:
\(E_1=\dfrac{9.10^9.4.10^{-8}}{\left(\dfrac{5}{100}\right)^2}=144000\left(v/m\right)\)
\(E_2=\dfrac{9.10^9.4.10^{-8}}{\left(\dfrac{15}{100}\right)^2}=16000\left(v/m\right)\)
\(\Rightarrow E=\left|E_1-E_2\right|=128000\left(v/m\right)\)

A B P d M d x d1 d2
\(d_1 - d_2 = \left( {\phi _m - \phi } \right)\dfrac{\lambda }{{2\pi }} = \left( {2k + 1} \right)\dfrac{{0.5\pi }}{{2\pi }} = \dfrac{k}{2} + 0.25 \)
Điểm M gần hất \(\Rightarrow k = 0 \Rightarrow d_1 - d_2 = 0.25 \)
\(\Rightarrow \sqrt {(\dfrac{d}{2} + x)^2 + 100^2 } - \sqrt {(\dfrac{d}{2} - x)^2 + 100^2 } = 0.25 \)
\(\Rightarrow \sqrt {(\dfrac{1}{2} + x)^2 + 100^2 } - \sqrt {(\dfrac{1}{2} - x)^2 + 100^2 } = 0.25 \)
\(\Rightarrow x = 25.82 m\)


Gọi H là trung điểm của AB và M là điểm nằm trên đường trung trực của AB.
Độ lớn hai điện tích bằng nhau và M cách đều hai điện tích.
Do \(E_1=E_2\) nên \(E=2E_1\cdot cos\alpha=2\cdot k\cdot q\cdot\dfrac{x}{\sqrt{\left(x^2+a^2\right)^2}}\)
\(E_{M_{max}}\Leftrightarrow\sqrt{\left(x^2+a^2\right)^2}_{min}\)
\(\Leftrightarrow x=a\)