Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi V là luu luong nuoc chay vao 2 bih ban dau. Binh 1 sau 2h van voi luu luong V thi tg de day bih 1 la: (375-2V)/V. Cug trong thoi jan nay nhung binh 2lai nghi 45m= .75h nhung bu lai chay luu luong V+ 25. => pt:
(375-2V)/V= .75+ (375-2v)/(V+25)... giai V=75

Gọi thời gian vòi 1 chảy một mình với công suất bình thường đầy bể là x giờ thời gian vòi 2 chảy một mình với công suất bình thường đầy bể là y giờ
ĐK: x, y > 12
Trong 1 giờ, vòi 1 chẩy được 1/x bể
Trong 1 giờ, vòi 2 chẩy được 1/y bể
Trong 1 giờ, cả hai vòi chẩy được 1/12 bể
Ta có phương trình: 1/x + 1/y = 1/12 (1)
Trong 8 giờ cả hai vòi chẩy được 8/12 bể hay 2/3 bể còn lại là 1/3 bể vòi 2 chẩy trong 3,5 giờ với năng suất là 2/y ta có phương trình:
3,5 . 2/y = 1/3 hay 7/y = 1/3 (2) Từ (1) và (2)
ta có hệ phương trình: {1/x + 1/y = 1/12 (1) {7/y = 1/3 (2)
Giải HPT này ta tìm được: x = 28 (tmđk) y = 21 (tmđk)
Vậy thời gian vòi 1 chảy một mình với công suất bình thường đầy bể là 28 giờ thời gian vòi 2 chảy một mình với công suất bình thường đầy bể là 21 giờ

Gọi thời gian vòi 1 chảy một mình đầy bể là x (h)
thời gian vòi 2 chảy một mình đầy bể là y(h)
ĐK : x > 6 ; y > 6
Ta có 1 giờ vòi 1 chảy được \(\dfrac{1}{x}\) (bể)
1 giờ vòi 2 chảy được \(\dfrac{1}{y}\)(bể)
1 giờ 2 vòi chảy được \(\dfrac{1}{6}\left(bể\right)\)
=> PT : \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\)(1)
mà vòi 1 chảy trong 2 giờ rồi khóa ; vòi 2 chảy tiếp 3 giờ được 40% bể
=> PT \(\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\)(2)
Từ (1) (2) => HPT : \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{3}\\\dfrac{2}{x}+\dfrac{3}{y}=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{1}{y}=\dfrac{1}{15}\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=10\\y=15\end{matrix}\right.\)(tm)
Vậy...

Gọi x(giờ) là thời gian vòi 1 chảy một mình đầy bể
Gọi y(giờ) là thời gian vòi 2 chảy một mình đầy bể
(Điều kiện: x>5; y>5)
Trong 1 giờ, vòi 1 chảy được: \(\dfrac{1}{x}\)(bể)
Trong 1 giờ, vòi 2 chảy được: \(\dfrac{1}{y}\)(bể)
Trong 1 giờ, hai vòi chảy được: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{5}\)(1)
Vì khi vòi thứ nhất chảy trong 3 giờ và vòi thứ 2 chảy trong 2 giờ thì được 12/25 bể nên ta có phương trình:
\(\dfrac{3}{x}+\dfrac{2}{y}=\dfrac{12}{25}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{5}\\\dfrac{3}{x}+\dfrac{2}{y}=\dfrac{12}{25}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{3}{5}\\\dfrac{3}{x}+\dfrac{2}{y}=\dfrac{12}{25}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{3}{25}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{3}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{25}{3}\\\dfrac{1}{x}=\dfrac{3}{5}-\dfrac{3}{25}=\dfrac{12}{25}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{25}{3}\\x=\dfrac{25}{12}\end{matrix}\right.\)(thỏa ĐK)
Vậy: Vòi 1 cần \(\dfrac{25}{12}h\) để chảy một mình đầy bể
Vòi 2 cần \(\dfrac{25}{3}h\) để chảy một mình đầy bể

Gọi thời gian vòi 1 chảy một mình với công suất bình thường đầy bể là x giờ
thời gian vòi 2 chảy một mình với công suất bình thường đầy bể là y giờ
ĐK: x, y > 12
Trong 1 giờ, vòi 1 chẩy được 1/x bể
Trong 1 giờ, vòi 2 chẩy được 1/y bể
Trong 1 giờ, cả hai vòi chẩy được 1/12 bể
Ta có phương trình: 1/x + 1/y = 1/12 (1)
Trong 8 giờ cả hai vòi chẩy được 8/12 bể hay 2/3 bể
còn lại là 1/3 bể vòi 2 chẩy trong 3,5 giờ với năng suất là 2/y
ta có phương trình: 3,5 . 2/y = 1/3
hay 7/y = 1/3 (2)
Từ (1) và (2) ta có hệ phương trình:
{1/x + 1/y = 1/12 (1)
{7/y = 1/3 (2)
Giải HPT này ta tìm được:
x = 28 (tmđk)
y = 21 (tmđk)
Vậy thời gian vòi 1 chảy một mình với công suất bình thường đầy bể là 28 giờ
thời gian vòi 2 chảy một mình với công suất bình thường đầy bể là 21 giờ

Gọi thời gian vòi thứ nhất chảy riêng đầy bể là x (giờ) (x>6)
thời gian vòi thứ hai chảy riêng đầy bể là y (giờ) (y>6)
Hai vòi nước cùng chảy vào một cái bể không có nước trong 6 giờ thì đầy bể
⇒ 1 x + 1 y = 1 6 (1)
vòi thứ nhất chảy trong 2 giờ, sau đó đóng lại và mở vòi thứ hai chảy tiếp trong 3 giờ nữa thì được 2/5 bể ⇒ 2. 1 x + 3. 1 y = 2 5 (2)
Từ (1) và (2) ta có hệ phương trình 1 x + 1 y = 1 6 2. 1 x + 3. 1 y = 2 5 ⇔ x = 10 y = 15
Đối chiếu với điều kiện, giá trị x=10; y=15 thỏa mãn.
Vậy thời gian vòi thứ nhất chảy riêng đầy bể là 10 giờ, thời gian vòi thứ hai chảy riêng đầy bể là 15 giờ.

Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là x (giờ), (x > 0)
Trong một giờ:
- Vòi thứ nhất chảy được 1/x (bể)
- Vòi thứ hai chảy được 1/(x+4) (bể)
- Vòi thứ ba chảy được 1/6 (bể)
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước ở bể chảy ra nên ta có phương trình:
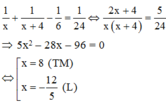
Vậy chỉ dùng vòi thứ nhất thì sau 8 giờ bể đầy nước
Đáp án: D
gọi V là lít nước chảy đc trong mỗi giờ
x là thời gian chảy còn lại đến khi cả 2 bình đều đầy
ta có hệ pt: \(\int^{2V+\frac{V}{45}+xV=375}_{2V+x\left(V+25\right)=375}\).
mk lập hpt thôi còn cậu tự bấm máy nhé, mà mk cũng ko chắc hpt của mk có đúng hay ko nữa
Nhân tung tóe rồi rút lui là xong