Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thầy tui cho cái ghi nhớ thế này \(\lim\limits\left(u_n-a\right)=0\Leftrightarrow\lim\limits u_n=a\) . Cơ mà theo tui cứ nên biến đổi từ từ đã :v
\(\lim\limits\left(\dfrac{1-4an+4a^2n^2-8an^2+4an-2a-16n^2+8n-4}{4n^2-2n+1}\right)\)
\(=\lim\limits\dfrac{4a^2n^2-8n^2\left(a+2\right)-2a+8n-3}{4n^2-2n+1}=\lim\limits\dfrac{4a^2-8\left(a+2\right)}{4}=0\Leftrightarrow a^2-2a-4=0\Leftrightarrow\left[{}\begin{matrix}a=1+\sqrt{5}\\a=1-\sqrt{5}\end{matrix}\right.\Rightarrow tong-S=2\)

\(A=lim\frac{\sqrt{n+2}+\sqrt{n+1}}{1}=lim\left[n\left(\sqrt{1+\frac{2}{n}}+\sqrt{1+\frac{1}{n}}\right)\right]=+\infty.2=+\infty\)
\(B=lim\frac{8^3.64^n-9.27^n}{4^4.64^n+5^3.25^n}=\frac{8^3-9.\left(\frac{27}{64}\right)^n}{4^4+5^3\left(\frac{25}{64}\right)^n}=\frac{8^3}{4^4}=2\)
\(1;-\frac{1}{2};\frac{1}{4}...\) là dãy cấp số nhân lùi vô hạn có \(u_1=1\) và \(q=-\frac{1}{2}\)
Do \(\left|q\right|< 1\) nên theo công thức tổng cấp số nhân:
\(S_n=\frac{u_1}{1-q}=\frac{1}{1+\frac{1}{2}}=\frac{2}{3}\)

Phương trình cos 2 x − π 3 − m = 2 ⇔ cos 2 x − π 3 = m + 2.
Phương trình có nghiệm ⇔ − 1 ≤ m + 2 ≤ 1 ⇔ − 3 ≤ m ≤ − 1
→ m ∈ ℤ S = − 3 ; − 2 ; − 1 ⇒ T = − 3 + − 2 + − 1 = − 6.
Chọn đáp án B.

Lời giải:
\(\lim\limits _{x\to 0}\frac{(x+a)^3-a^3}{x}=\lim\limits _{x\to 0}\frac{x[(x+a)^2+a(x+a)+a^2]}{x}=\lim\limits _{x\to 0}[(x+a)^2+a(x+a)+a^2]\)
\(=3a^2\)
Để \(\lim\limits _{x\to 0}\frac{(x+a)^3-a^3}{x}=a\) \(\Leftrightarrow 3a^2=a\)
\(\Leftrightarrow 3a^2-a=0\Leftrightarrow a=0; a=\frac{1}{3}\) (có 2 giá trị thực của a)
Đáp án A.

Số tập hợp con có k phần tử của tập hợp A (có 18 phần tử)
\(C_{18}^k\left(k=1,.....,18\right)\)
Để tìm max \(C_{18}^k,k\in\left\{1,2,.....,18\right\}\) (*), ta tiến hành giải bất phương trình sau :
\(\frac{C_{18}^k}{C_{18}^{k+1}}< 1\)
\(\Leftrightarrow C_{18}^k< C_{18}^{k+1}\)
\(\Leftrightarrow\frac{18!}{\left(18-k\right)!k!}< \frac{18!}{\left(17-k\right)!\left(k+1\right)!}\)
\(\Leftrightarrow\left(18-k\right)!k!>\left(17-k\right)!\left(k+1\right)!\)
\(\Leftrightarrow17>2k\)
\(\Leftrightarrow k< \frac{17}{2}\)
Điều kiện (*) nên k = 1,2,3,.....8
Suy ra \(\frac{C_{18}^k}{C_{18}^{k+1}}>1\) khi k = 9,10,...,17
Vậy ta có
\(C^1_{18}< C_{18}^2< C_{18}^3< .........C_{18}^8< C_{18}^9>C_{18}^{10}>.....>C_{18}^{18}\)
Vậy \(C_{18}^k\) đạt giá trị lớn nhất khi k = 9. Như thế số tập hợp con gồm 9 phần tử của A là số tập hợp con lớn nhất.

Đáp án C
Ta tìm số cặp số (a;b) thoả mãn
![]()
![]()
Có 49 cặp (a;b) thỏa mãn. Do đó S gồm 49 phần tử:
Ta tìm số cặp (a;b) thoả mãn
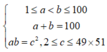
![]()
Do đó 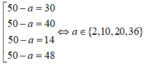
Vậy có 4 cặp số (a;b)có tổng bằng 100 và tích của chúng là một số chính phương.

a) Cả tử số và mẫu số của \(\frac{7n^2-3n+12}{n^2+2n+2}\) đều dẫn đến \(\infty\) nên không thể trả lời ngay biểu thức đó tiến đến giới hạn nào (dạng vô định \(\left(\frac{\infty}{\infty}\right)\)). Tuy nhiên sau khi chia cả tử số và mẫu số cho \(n^2\) :
\(\frac{7n^2-3n+12}{n^2+2n+2}=\frac{7-\frac{3}{n}+\frac{12}{n^2}}{1+\frac{2}{n}+\frac{2}{n^2}}\)
Ta thấy ngay tử số gần đến 7 và mẫu số gần đến 1 (vì \(\lim\limits\frac{1}{n^p}=0,p\ge1\)
Điều đó cho phép ta áp dụng công thức và thu được kết quả \(\lim\limits\frac{7n^2-3n+12}{n^2+2n+2}=\lim\limits\frac{7-\frac{3}{n}+\frac{12}{n^2}}{1+\frac{2}{n}+\frac{2}{n^2}}=7\)
b) Áp dụng công thức "Nếu tồn tại \(\lim\limits a^n,k\in\)N* thì tồn tại \(\lim\limits\left(a_n\right)^k=\left(\lim\limits a_n\right)^k\)"
ta có :
\(\lim\limits a_n=\left[\lim\limits\left(\frac{3n^2+n-2}{4n^2+2n+7}\right)\right]^3\)
Mặt khác do \(\lim\limits\frac{3n^2+n-2}{4n^2+2n+7}=\lim\limits\frac{3+\frac{1}{n}-\frac{2}{n^2}}{4+\frac{2}{n}+\frac{7}{n^2}}=\frac{3}{4}\)
nên \(\lim\limits a_n=\left(\frac{3}{4}\right)^3=\frac{27}{64}\)
\(lim\left(\frac{3n+2}{n+2}+a^2-4a\right)=lim\left(\frac{3+\frac{2}{n}}{1+\frac{2}{n}}+a^2-4a\right)=a^2-4a+3\)
\(\Rightarrow a^2-4a+3=0\Rightarrow\left[{}\begin{matrix}a=1\\a=3\end{matrix}\right.\)
\(\Rightarrow S=4\)