Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

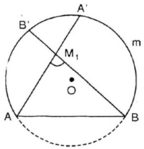
M 1 là điểm bất kì nằm trong cung chưa góc 55 o
Gọi A' và B' lần lượt là giao điểm của M 1 A , M 1 B với đường tròn. Vì góc A M 1 B ^ là góc có đỉnh nằm trong đường tròn nên:
A M 1 B ^ = 1 2 . s đ A B ⏜ + s đ A ' B ' ⏜ = 1 2 s đ A B ⏜ + 1 2 s đ A ' B ' ⏜ = 1 2 . 110 o + m ộ t s ố d ư ơ n g = 55 o + m ộ t s ố d ư ơ n g > 55 o
(Điều phải chứng minh)

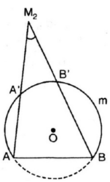
Điểm M 2 là điểm nằm ngòi đường tròn
Gọi M 2 A v à M 2 B là góc có đỉnh nằm ngoài đường tròn nên:
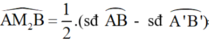

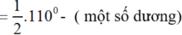
![]()

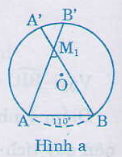
M1 là điểm bất kì nằm trong cung chứa góc 550 (hình a).
Gọi B’, A’ theo thứ tự là giao điểm của M1A, M1B với cung tròn. Vì góc AM1B là góc có đỉnh nằm trong đường tròn, nên: góc AM1B = sđ cung(AB +A’B’)/2 = sđcung AB/2 + sđcung A’B’/2 = 550+ (một số dương) Vậy góc AM1B > 550
b)
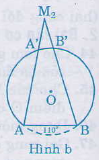
M2 là điểm bất kì nằm ngoài đường tròn (h.b), M2A, M2B lần lượt cắt đường tròn tại A’, B’. Vì góc AM2B là góc có đỉnh nằm bên ngoài đường tròn nên: góc AM2B= sđcung(AB – A’B’)/2= sđAB/2 – sđA’B’/2 = 550 – (một số dương)
Vậy góc AM2B < 550
M1 là điểm bất kì nằm trong cung chứa góc 550 .
Gọi B’, A’ theo thứ tự là giao điểm của M1A, M1B với cung tròn. Vì góc AM1B là góc có đỉnh nằm trong đường tròn, nên: góc AM1B = sđ cung(AB +A’B’)/2 = sđcung AB/2 + sđcung A’B’/2 = 550+ (một số dương)
Vậy góc AM1B > 550
b)
M2 là điểm bất kì nằm ngoài đường tròn , M2A, M2B lần lượt cắt đường tròn tại A’, B’. Vì góc AM2B là góc có đỉnh nằm bên ngoài đường tròn nên: góc AM2B= sđcung(AB – A’B’)/2= sđAB/2 – sđA’B’/2 = 550 – (một số dương)
Vậy góc AM2B < 550

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay ΔAMB cân tại M
hay \(\widehat{AMB}=60^0\)
nên ΔAMB đều
b: Xét (O) có
NA là tiếp tuyến
NC là tiếp tuyến
Do đó: ON là tia phân giác của góc AOC(1)
Xét (O) có
QC là tiếp tuyến
QB là tiếp tuyến
Do đó: OQ là tia phân giác của góc NOB(2)
Từ (1) và (2) suy ra \(\widehat{NOQ}=\dfrac{1}{2}\cdot120^0=60^0\)

Bài 1 thiếu đề
Bài 2 Mình không vẽ được hình nên bạn thông cảm
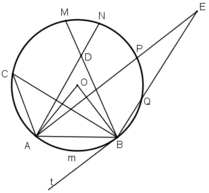
Xét tam giác vuông ACO có \(CM\perp AO\)
=> \(OM.OA=OC^2=OD^2\)
=> \(\frac{OD}{OA}=\frac{OM}{OD}\)
=> tam giác MDO đồng dạng tam giác DAO
=> MDO=OAD
Mà MDO=DEO
=> OAD=DEO
=> tứ giác ADOE nội tiếp
Vậy tứ giác ADOE nội tiếp
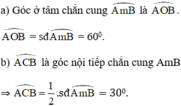

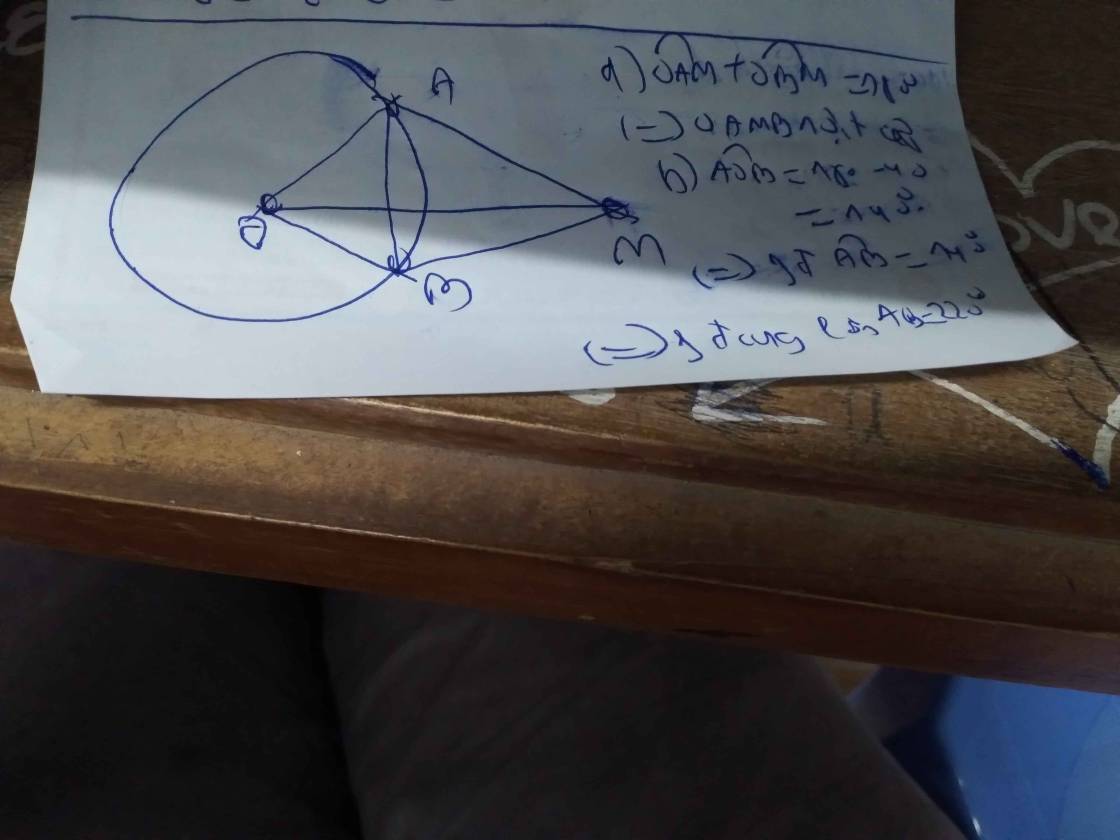
Kiến thức áp dụng
+ Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn
+ Số đo của góc có đỉnh nằm bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn