
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi độ dài hai cạnh góc vuông lần lượt là a(m),b(m)(ĐK: a>0;b>0)
Độ dài hai cạnh góc vuông tỉ lệ với 3 và 4 nên \(\dfrac{a}{3}=\dfrac{b}{4}=k\)
=>a=3k; b=4k
Theo đề, ta có: \(a^2+b^2=20^2\)
=>\(25k^2=400\)
=>\(k^2=16\)
=>k=4
=>a=3*4=12; b=4*4=16

#)Giải :
A B C H
Áp dụng định lí Py - ta - go :
\(BC^2=AB^2+AC^2\Leftrightarrow BC^2=3^2+4^2=9+16=25\)
\(\Rightarrow BC=\sqrt{25}=5\)
Ta có : \(AB.AC=BC.AH\)
\(\Rightarrow3.4=5.AH\Rightarrow H=\frac{12}{5}\)
\(\hept{\begin{cases}AB^2=BC.BH\Rightarrow BH=\frac{AB^2}{BC}=\frac{3^2}{5}=\frac{9}{5}\\AC^2=BC.CH\Rightarrow CH=\frac{AC^2}{BC}=\frac{4^2}{5}=\frac{16}{5}\end{cases}}\)
Vậy \(\hept{\begin{cases}BC=5\\BH=\frac{9}{15}\\CH=\frac{16}{5}\end{cases}}\)

Gọi độ dài cạnh góc vuông nhỏ là x (m)(x > 0)
Độ dài cạnh góc vuông lớn là x + 8 (m)
Khi tăng độ dài cạnh góc vuông nhỏ lên 2 lần ta được cạnh có độ dài 2x (m)
Khi giảm độ dài cạnh góc vuông còn lại xuống 3 lần thì được cạnh có độ dài 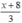 (m)
(m)
Tam giác vuông mới có diện tích bằng 51 m 2
Theo công thức tính diện tích tam giác vuông ta có phương trình:
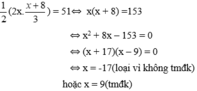
Vậy độ dài cạnh góc vuông nhỏ là 9m. Độ dài cạnh góc vuông lớn là 17m.

Xét tam giác ABC có ba cạnh BC = a, CA = b, AB = c. Phân giác của các góc A, B, C lần lượt là AD = x, BE = y, CF = z.
Kẻ DM // AB \((M\in AC)\).
Ta có \(\widehat{ADM}=\widehat{BAD}=\widehat{MAD}\Rightarrow\) Tam giác AMD cân tại M.
Do đó AM = MD.
Áp dụng định lý Thales với DM // AB ta có:
\(\dfrac{MD}{AB}=\dfrac{CM}{AC}=1-\dfrac{AM}{AC}=1-\dfrac{DM}{AC}\Rightarrow\dfrac{MD}{AB}+\dfrac{MD}{AC}=1\Rightarrow\dfrac{1}{MD}=\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{1}{b}+\dfrac{1}{c}\).
Mặt khác theo bất đẳng thức tam giác ta có \(x=AD< AM+MD=2MD\Rightarrow MD>\dfrac{x}{2}\Rightarrow\dfrac{1}{MD}< \dfrac{2}{x}\Rightarrow\dfrac{1}{b}+\dfrac{1}{c}< \dfrac{2}{x}\).
Tương tự \(\dfrac{1}{c}+\dfrac{1}{a}< \dfrac{2}{y};\dfrac{1}{a}+\dfrac{1}{b}< \dfrac{2}{z}\).
Cộng vế với vế của các bđt trên rồi rút gọn ta có đpcm.

A E B D C x b c c A
Từ B kẻ đường thẳng song song với đường phân giác AD, cắt CA ở E. Tam giác ABE cân ở A nên AE = AB = c
\(\Rightarrow\)CE = CA + AE = b + c
Do đó AD // BE nên ta có :
\(\frac{AD}{BE}=\frac{CA}{CE}\)hay \(\frac{x}{BE}=\frac{b}{b+c}\), do đó \(x=\frac{b}{b+c}.BE\)
Mà BE < AB + AC < 2c
\(\Rightarrow\) \(x< \frac{2bc}{b+c}\)hay \(\frac{1}{x}>\frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}\right)\)( 1 )
Tương tự ta có : \(\frac{1}{y}>\frac{1}{2}\left(\frac{1}{c}+\frac{1}{a}\right)\)( 2 )
ta cũng có : \(\frac{1}{z}>\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)\)( 3 )
Cộng từng vế của ( 1 ) ; ( 2 ) ; ( 3 ) ta có :
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}>\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
Vậy \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}>\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\left(ĐPCM\right)\)
Hình mình vẽ hơi xấu tí thông cảm