
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1: Xét ΔABD vuông tại A và ΔDAC vuông tại D có
góc ABD=góc DAC
=>ΔABD đồng dạng với ΔDAC
2: ΔABD đồng dạng với ΔDAC
=>BD/AC=AB/DA=AD/DC
=>AD/16=BD/AC=18/DA
=>AD^2=16*18=288
=>AD=12căn 2(cm)
AC=căn AD^2+DC^2=4căn 82(cm)

a) \(\dfrac{A}{x-2}=\dfrac{x^2+3x+2}{x^2-4}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{x+1}{x-2}\Leftrightarrow A=x+1\)
b) \(\dfrac{M}{x-1}=\dfrac{x^2+3x+2}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=\dfrac{\left(x+1\right)\left(x+2\right)}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=x+2\Leftrightarrow M=\left(x-1\right)\left(x+2\right)=x^2+x-2\)

(3x-4-x-1)(3x-4+x+1)=0
(2x-5)(4x-3)=0
2x-5 = 0 hoặc 4x-3=0
2x=5 hoặc 4x=3
x=5/2 hoặc x=3/4



Trả lời:
Bài 1:
a, \(9x^2-4=\left(3x\right)^2-2^2=\left(3x-2\right)\left(3x+2\right)\)
b, \(x^3+27=x^3+3^3=\left(x+3\right)\left(x^2-3x+9\right)\)
c, \(8-y^3=2^3-y^3=\left(2-y\right)\left(4+2y+y^2\right)\)
d, \(x^4-81=\left(x^2\right)^2-9^2=\left(x^2-9\right)\left(x^2+9\right)\)\(=\left(x^2-3^2\right)\left(x^2+9\right)=\left(x-3\right)\left(x+3\right)\left(x^2+9\right)\)
e, \(64x^3-1=\left(4x\right)^3-1^3=\left(4x-1\right)\left(16x^2+4x+1\right)\)
f, \(x^6+8y^3=\left(x^2\right)^3+\left(2y\right)^3=\left(x^2+2y\right)\left(x^4-2x^2y+4y^2\right)\)

Bài 2:
a: =>168x+20=6x-21
=>162x=-41
hay x=-41/162
b: \(\Leftrightarrow2\left(3x-8\right)=3\left(5-x\right)\)
=>6x-16=15-3x
=>9x=31
hay x=31/9
c: \(\Leftrightarrow4\left(x^2+8x-20\right)-\left(x+4\right)\left(x+10\right)=3\left(x^2+2x-8\right)\)
\(\Leftrightarrow4x^2+32x-80-x^2-14x-40-3x^2-6x+24=0\)
=>12x-96=0
hay x=8

 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ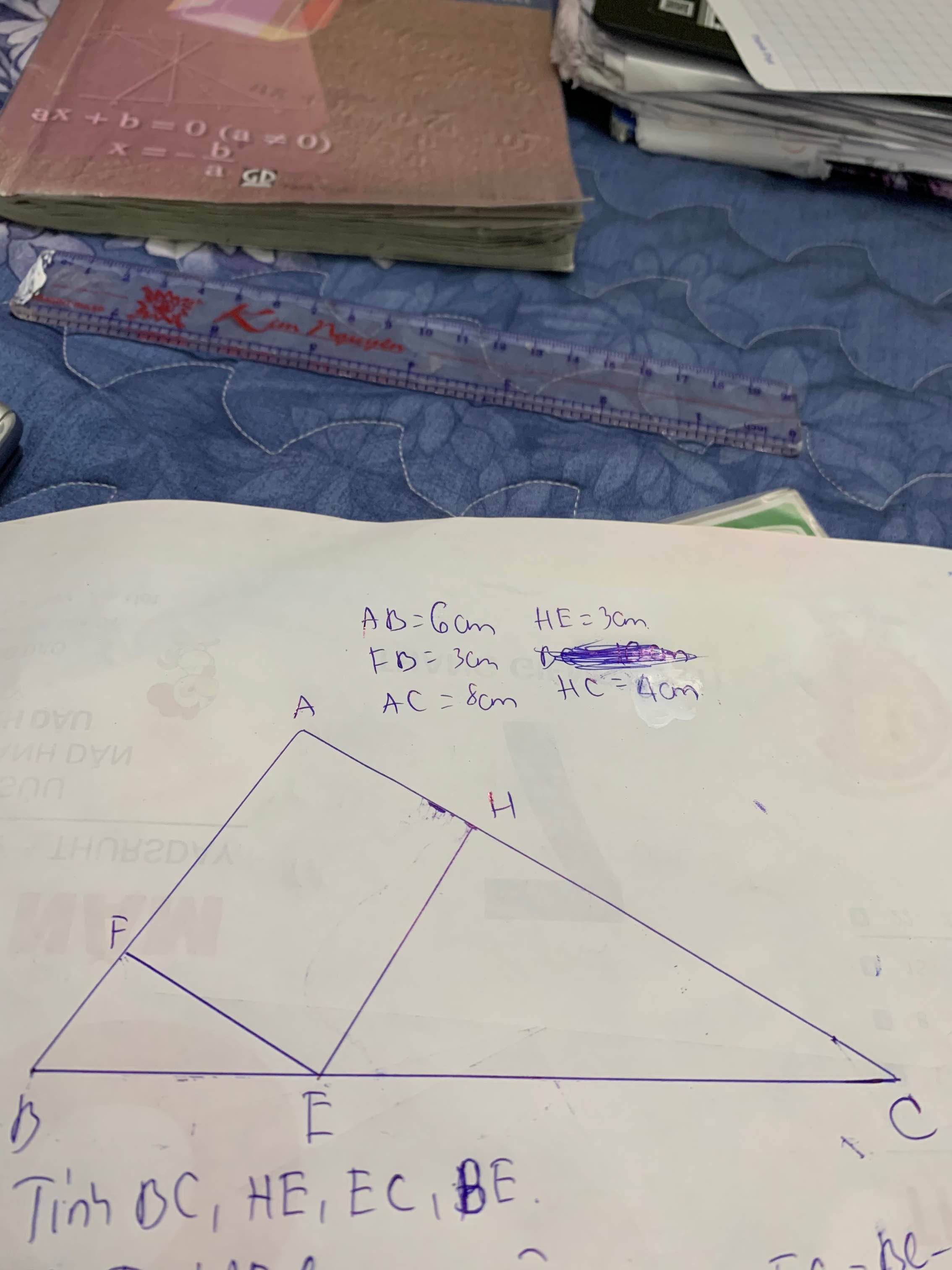
 lúc 5h
lúc 5h