K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 10 2017
\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
Vì \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge0\forall x\\\left|y^2-9\right|\ge0\forall y\end{matrix}\right.\)
để bt = 0 \(\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\y^2-9=0\Rightarrow y^2=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy.....
24 tháng 10 2017
\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\y^2-9=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\y^2=9\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=3\\y=3hoặcy=-3\end{matrix}\right.\)
IM
21 tháng 2 2017
Ta có :
\(S=1.2+2.3+...+49.50\)
\(\Leftrightarrow3S=1.2.\left(3-0\right)+2.3.\left(4-1\right)+...+49.50.\left(51-48\right)\)
\(\Leftrightarrow3S=1.2.3-0.1.2+2.3.4-1.2.3+...+49.50.51-48.49.50\)
\(\Leftrightarrow3S=49.50.51\)
\(\Leftrightarrow S=\frac{49.50.51}{3}=41650\)
21 tháng 2 2017
S=1 . 2 + 2.3+3.4+.....+49.100
3S=1.2.3+2.3.3+3.4.3+....+49.50.3
3S=1.2.3+2.3.(4-1)+3.4(5-2)+....+49.50(51-48)
3S=1.2.3-2.3.4+2.3.4-2.3.1+......+48.49.50+49.50.51
3S=49.50.51
S=49.50.51 / 3
S=41650
S
5 tháng 2 2017
\(\)\(A=2^0+2^1+2^2+2^3+...+2^{2012}\\ A=1+2+\left(2^2+2^3+2^4\right)+\left(2^5+2^6+2^7\right)+...+\left(2^{2010}+2^{2011}+2^{2012}\right)\\ A=3+2^2\cdot\left(1+2+2^2\right)+2^5\cdot\left(1+2+2^2\right)+...+2^{2010}\cdot\left(1+2+2^2\right)\\ A=3+2^2\cdot\left(1+2+4\right)+2^5\cdot\left(1+2+4\right)+...+2^{2010}\cdot\left(1+2+4\right)\\ A=3+2^2\cdot7+2^5\cdot7+...+2^{2010}\cdot7\\ A=3+7\cdot\left(2^2+2^5+...+2^{2010}\right)\\ \)
YN
17 tháng 2 2017
Ta có : \(\left\{\begin{matrix}Q=-\left(x-7\right)^2-6\\-\left(x-7\right)^2\le0\\-6=-6\end{matrix}\right.\)
\(\Rightarrow Q=-\left(x-7\right)^2-6\le0-6=-6\)
Vậy GTLN của \(Q=-\left(x-7\right)^2-6\) là \(-6\)
IM
21 tháng 2 2017
Ta có :
\(2015^{2014}=\left(\overline{......5}\right)\)
\(2014^{2015}=\left(2014^4\right)^{503}.\left(2014^3\right)=\left(\overline{.....6}\right).\left(\overline{.....4}\right)=\left(\overline{.....4}\right)\)
\(2015^{2014}-2014^{2015}=\left(\overline{......5}\right)-\left(\overline{......4}\right)=\left(\overline{......1}\right)\)
Vậy biểu thức có chữ số tận cùng là 1
MP
21 tháng 2 2017
Ta có:
- \(2015^{2014}\) có chữ số tận cùng là 5 (Các số có tận cùng là 5 khi nâng lên lũy thừa bậc mấy chữ số tận cùng cũng không thay đổi)
- \(2014^{2015}\) có chữ số tận cùng là 4 (Các số có tận cùng là 4 khi nâng lên lũy thừa bậc lẻ thì chữ số tận cùng không thay đổi)
~> \(2015^{2014}-2014^{2015}=5-4=1\)
Vậy, chữ số tận cùng của \(2015^{2014}-2014^{2015}\) là 1
---
Chọn đáp án này đi :)
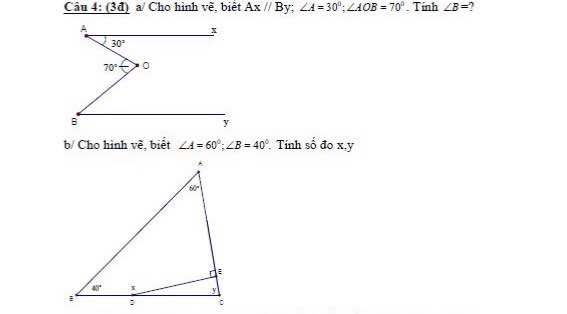
Câu 4a.
Kẻ tia $Om\parallel Ax$ như hình:
Vì $Ax\parallel Om$ nên $\widehat{AOm}=\widehat{xAO}=30^0$ (hai góc so le trong)
$\Rightarrow \widehat{mOB}=\widehat{AOB}-\widehat{AOm}=70^0-30^0=40^0$
$Ax\parallel By, Ax\parallel Om\Rightarrow By\parallel Om$
$\Rightarrow \widehat{B}=\widehat{mOB}=40^0$ (hai góc so le trong)
a) Trên nửa mặt phẳng bờ OB chứa điểm A, kẻ tia Oz//Ax//By
Ta có: Oz//Ax(cách vẽ)
\(\Rightarrow\widehat{xAO}=\widehat{AOz}=30^0\)( 2 góc so le trong)
Ta có: \(\widehat{AOz}+\widehat{zOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{zOB}=\widehat{AOB}-\widehat{AOz}=70^0-30^0=40^0\)
Ta có: Oz//By
\(\Rightarrow\widehat{B}=\widehat{zOB}=40^0\)( 2 góc so le trong)
b) Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-40^0=80^0\)
\(\Rightarrow y=80^0\)
Xét tứ giác AEDB có:
\(\widehat{AED}+\widehat{EDB}+\widehat{ABD}+\widehat{BAE}=360^0\)
\(\Rightarrow\widehat{EDB}=360^0-\widehat{AED}-\widehat{ABD}-\widehat{BAE}=360^0-90^0-40^0-60^0=170^0\)
\(\Rightarrow x=170^0\)