Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vị trí ảnh:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\Rightarrow d'=60cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{20}{h'}=\dfrac{30}{60}\Rightarrow h'=40cm\)

Ảnh thật, nhỏ hơn vật, cùng chiều với vật.
Nơi có ảnh cách thấu kính một đoạn:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{60}+\dfrac{1}{d'}\)
\(\Rightarrow d'=30cm\)
Độ lớn ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{4}{h'}=\dfrac{60}{30}\Rightarrow h'=2cm\)

Tham khảo:
Ảnh thật, ngược chiều, lớn hơn vật và cách thấu kính một khoảng 60cm.
Lời giải: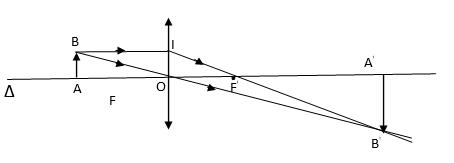
giải tính chiều cao:
ΔOAB ∼ ΔOA'B'
=> \(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\left(1\right)\)
ta lại có :
Δ OIF ∼ Δ A'B'F'
=> \(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'B'}\left(2\right)\)
Từ (1) và (2) suy ra : \(\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}\left(3\right)\)
mà : A'F' = OA' - OF ' (4)
thay số vào (3) và (4) ta được : OA' = 60cm