K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NK
2
NQ
5
TT
2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
6 tháng 1 2022
\(=3^4.\left(3^3\right)^4+3^2.\left(3^4\right)^3=3^{16}+3^2.\left(3^4\right)^3=\left(3^4\right)^4+3^2.\left(3^4\right)^3\)
\(3^4\) có tận cùng là 1 \(\Rightarrow\left(3^4\right)^4\) có tận cùng là 1
\(3^4\)có tận cùng là 1 \(\Rightarrow\left(3^4\right)^3\) có tận cùng là 1 \(\Rightarrow3^2.\left(3^4\right)^3\) có tận cùng là 9
=> Biểu thức có tận cùng là 0
VC
3
GR
8 tháng 10 2017
Chỗ chấm là 3 nhé
Mình đổi chỗ chấm thành x nha
\(\left(\frac{1}{x}\right)^5=\frac{3}{96}\)
\(\Rightarrow\frac{1}{x^5}=\frac{1}{32}\)\(\Rightarrow x^5=32\Rightarrow x^5=3^5\Rightarrow x=3\)
LN
10 tháng 7 2019
Có: \(a^2+b+2=2ab\)
\(\Leftrightarrow a^2+2=b\left(2a-1\right)\)
\(\Leftrightarrow b=\frac{a^2+2}{2a-1}\in Z\)
khi và chỉ khi \(a^2+2⋮2a-1\)
\(\Leftrightarrow2\left(a^2+2\right)-a\left(2a-1\right)⋮2a-1\)
\(\Leftrightarrow a+4⋮2a-1\)
\(\Leftrightarrow2\left(a+4\right)-\left(2a-1\right)⋮2a-1\)
\(\Leftrightarrow9⋮2a-1\)
\(\Leftrightarrow2a-1\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)
Rồi giải a..........
Rồi giải b...........
Bước tiếp theo bn giải nha
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
10 tháng 11 2016
Đặt vế trái phương trình là A
\(3A=\frac{3}{1.4}+\frac{3}{4.7}+\frac{3}{7.10}+...+\frac{3}{x\left(x+3\right)}\)
\(3A=\frac{4-1}{1.4}+\frac{7-4}{4.7}+\frac{10-7}{7.10}+\frac{\left(x+3\right)-x}{x\left(x+3\right)}\)
\(3A=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+...+\frac{1}{x}-\frac{1}{x+3}\)
\(3A=1-\frac{1}{x+3}=\frac{x+2}{x+3}\Rightarrow A=\frac{x+2}{3\left(x+3\right)}\)
\(\Rightarrow\frac{x+2}{3\left(x+3\right)}=\frac{667}{2002}\Rightarrow2002\left(x+2\right)=3.667.\left(x+3\right)\)
\(\Leftrightarrow2002x+4004=2001x+6003\Leftrightarrow x=1999\)
DC
0
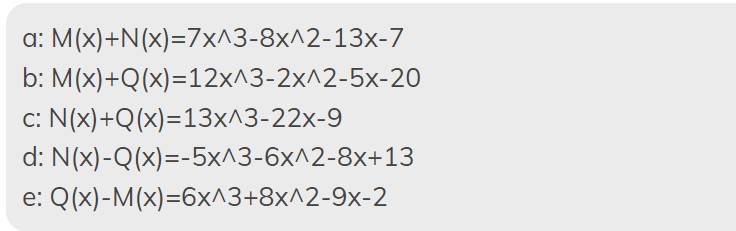
tham khảo
?????????