Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:

a) Xét \(\Delta ABH\) vuông tại \(H\left(gt\right)\) có:
\(AH^2+BH^2=AB^2\) (định lí Py - ta - go).
=> \(12^2+BH^2=15^2\)
=> \(BH^2=15^2-12^2\)
=> \(BH^2=225-144\)
=> \(BH^2=81\)
=> \(BH=9\left(cm\right)\) (vì \(BH>0\)).
+ Xét \(\Delta ACH\) vuông tại \(H\left(gt\right)\) có:
\(AH^2+HC^2=AC^2\) (định lí Py - ta - go).
=> \(12^2+HC^2=20^2\)
=> \(HC^2=20^2-12^2\)
=> \(HC^2=400-144\)
=> \(HC^2=256\)
=> \(HC=16\left(cm\right)\) (vì \(HC>0\)).
b) Ta có: \(BC=BH+HC.\)
=> \(BC=9+16\)
=> \(BC=25\left(cm\right).\)
+ Xét \(\Delta ABC\) có:
\(AB^2+AC^2=15^2+20^2\)
=> \(AB^2+AC^2=225+400\)
=> \(AB^2+AC^2=625\) (1).
\(BC^2=25^2\)
=> \(BC^2=625\) (2).
Từ (1) và (2) => \(AB^2+AC^2=BC^2\left(=625\right).\)
=> \(\Delta ABC\) vuông tại \(A\) (định lí Py - ta - go đảo) (đpcm).
Chúc bạn học tốt!

A B D C H K
a) Xét \(\bigtriangleup ABC\) cân tại A, có:
AD là đường cao của cạnh BC
=> AD cũng là đường trung tuyến của cạnh BC
=> D là trung điểm của cạnh BC
Hay: BD = CD
b) Ta có: AD là đường cao của \(\bigtriangleup ABC\) cân tại A
Nên: AD cũng là đường phân giác của \(\bigtriangleup ABC\)
=> \(\widehat{BAD}=\widehat{CAD}\)
Hay: \(\widehat{HAD}=\widehat{KAD}\)
Xét \(\bigtriangleup AHD\) và \(\bigtriangleup AKD\):
Ta có: \(\left\{\begin{matrix} \widehat{AHD}=\widehat{AKD}=90^{\circ}(DH\perp AB,DK\perp AC) & & & \\ AD:chung & & & \\ \widehat{HAD}=\widehat{KAD}(cmt) & & & \end{matrix}\right.\)
Vậy: \(\bigtriangleup AHD=\bigtriangleup AKD(ch-gn)\)
=> DH = DK
c) \(\bigtriangleup AHD=\bigtriangleup AKD(cmt)\)
=> AH = AK
=> \(\bigtriangleup AHK\) cân tại A
=> \(\widehat{AKH}=\frac{180^{\circ}-\widehat{BAC}}{2}\)
Mà: \(\widehat{ACB}=\frac{180^{\circ}-\widehat{BAC}}{2}\)
Nên: \(\widehat{AKH}=\widehat{ACB}\)
(nằm ở vị trí đồng vị)
=> HK // BC
d) Ta có: BD = DC = \(\dfrac{BC}{2}=\dfrac{12}{2}=6\) cm
Xét \(\bigtriangleup ADB\) vuông tại D (AD đường cao), ta có:
\(AD^2=AB^2-BD^2\left(Py-ta-go\right)\)
\(AD^2=10^2-6^2=64\)
\(\Rightarrow AD=\sqrt{64}=8cm\)

bạn tự vẽ hình, ghi gt và kl nha.
MÌNH GHI TẮT NHA: TG là tam giác, ^ là mũ
a. Xét 2 TG vuông ADB và ADC, có:
AB = AC ( gt)
AD cạnh chung
=> TG vuông ADB = TG vuông ADC ( ch - cgv)
=> BD = CD ( 2 cạnh tương ứng)
d. Ta có: BD = 1/2 x BC = 1/2 x 12 = 6(cm)
áp dụng d/l pytago cho TG vuông ADB và ABC;
ta có: AD^2 = AB^2 + AC^2
hay AD^2 = 10^2 + 6^2
= 100+36
= 136
=. AD = căn 136

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!!!!!!!!!!!!!!!!111
a, xét tam giác tam giác ADB và am giác ADC:
Ab=ac (gt)
ad chung
góc adc = góc adb=90 độ (gt)

A B C 6 10 D H K
a, Xét \(\Delta ABC\)VUÔNG tại A
Áp dụng định lý pitago ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\)
\(\Rightarrow AB^2=10^2-6^2\)
\(\Rightarrow AB^2=100-36\)
\(\Rightarrow AB^2=64\)
\(\Rightarrow AB=\sqrt{64}=8\)
VẬY AB=8 cm
b, Xét \(\Delta ABD\)và \(\Delta HBD\)CÓ:
\(\widehat{BAD}=\widehat{BHD}=90độ\)
\(\widehat{ABD}=\widehat{HBD}\)(do BD là tia phân giác của \(\widehat{B}\))
BD là cạnh chung
\(\Rightarrow\Delta ABD=\Delta HBD\)(ch-gn)
\(\Rightarrow AD=HD\)(2 CẠNH TƯƠNG ỨNG)
c,Do \(\Delta ABD=\Delta HBD\left(câub\right)\)
\(\Rightarrow\widehat{BDA}=\widehat{BDH}\)(2 góc tương ứng)
lại có \(\widehat{ADK}=\widehat{HDC}\)(đối đỉnh)
\(\Rightarrow\widehat{BDA}+\widehat{ADK}=\widehat{BDH}+\widehat{HDC}\)
\(\Rightarrow\widehat{BDK}=\widehat{BDC}\)
Xét \(\Delta KBD\) VÀ \(\Delta CBD\)CÓ:
\(\widehat{ABD}=\widehat{CBD}\)(Do BD là tia phân giác của \(\widehat{B}\))
BD là cạnh chung
\(\widehat{BDK}=\widehat{BDC}\left(cmt\right)\)
Do đó \(\Delta KBD=\Delta CBD\left(g-c-g\right)\)
\(\Rightarrow BK=BC\)(2 CẠNH TƯƠNG ỨNG)
\(\Rightarrow\Delta KBC\) cân tại B
 BC).
BC).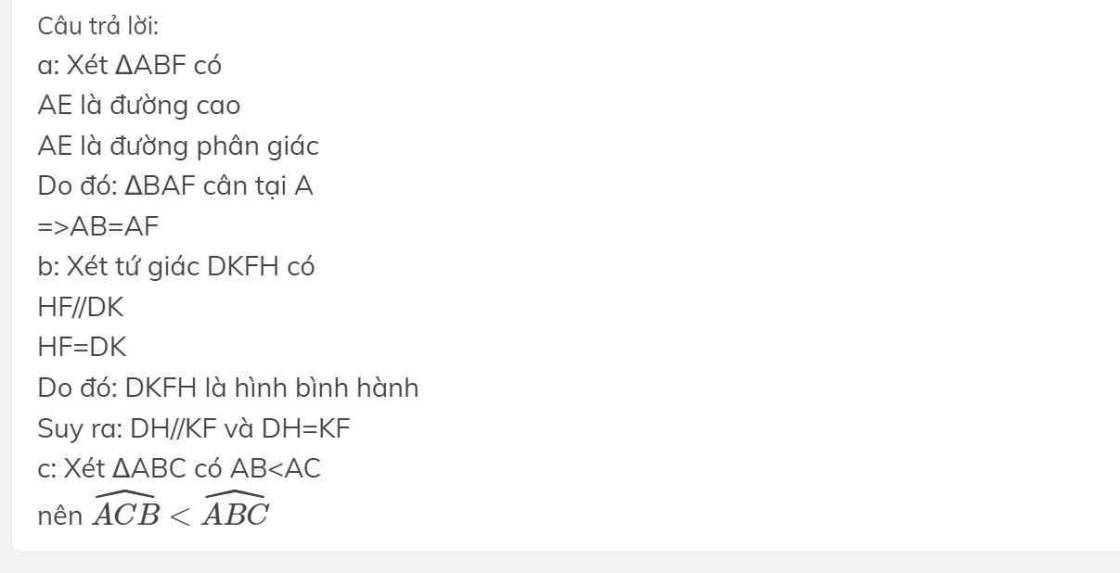
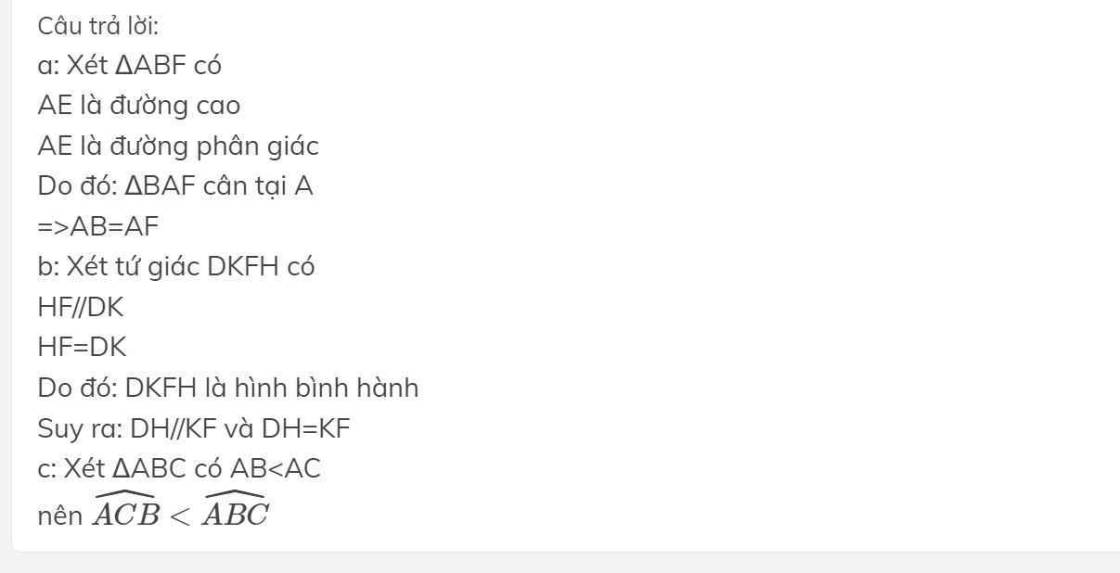
a) Xét ΔABD vuông tại D và ΔACD vuông tại D có
AB=AC(ΔABC cân tại A)
AD là cạnh chung
Do đó: ΔABD=ΔACD(cạnh huyền-cạnh góc vuông)
⇒BD=CD(hai cạnh tương ứng)
b) Xét ΔHBD vuông tại H và ΔKCD vuông tại K có
BD=CD(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔHBD=ΔKCD(cạnh huyền-góc nhọn)
⇒DH=DK(hai cạnh tương ứng)
c) Ta có: AH+HB=AB(H nằm giữa A và B)
AK+KC=AC(K nằm giữa A và C)
mà AB=AC(ΔABC cân tại A)
và BH=KC(ΔHBD=ΔKCD)
nên AH=AK
Xét ΔAHK có AH=AK(cmt)
nên ΔAHK cân tại A(định nghĩa tam giác cân)
⇒\(\widehat{AHK}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy của ΔAHK cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
⇒\(\widehat{B}=\frac{180^0-\widehat{A}}{2}\)(số đo của một góc ở đáy của ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AHK}=\widehat{B}\)
mà \(\widehat{AHK}\) và \(\widehat{B}\) là hai góc ở vị trí đồng vị
nên HK//BC(dấu hiệu nhận biết hai đường thẳng song song)
d) Ta có: BD+CD=BC=12cm(D nằm giữa B và C)
mà BD=CD(cmt)
nên \(BD=\frac{BC}{2}=\frac{12}{2}=6cm\)
Áp dụng định lí pytago vào ΔABD vuông tại D, ta được
\(AB^2=BD^2+AD^2\)
hay \(AD^2=AB^2-BD^2=10^2-6^2=64\)
⇒\(AD=\sqrt{64}=8cm\)
Vậy: AD=8cm