Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nguyễn Hữu Giang Y hệt như cái cách mình làm câu a, chỉ thay số khác đi thôi mà :(
\(F_{13}=\frac{k\left|q_1q_3\right|}{r_{13}^2}=...\)\(;F_{23}=\frac{k\left|q_2q_3\right|}{r_{23}^2}=....\)
Vậy lực tác dụng lên q3 là:\(\Rightarrow\sum F_3=\sqrt{F_{13}^2+F_{23}^2+2F_{13}.F_{23}.\cos\left(60^0\right)}\)
Làm tương tự để tính lực t/d các đt còn lại, câu b cũng vậy thôi

Ta có: BC = A B 2 + A C 2 = 15 cm. Các điện tích q 1 v à q 2 tác dụng lên q 3 các lực F 1 → và F 2 → .
Lực tổng hợp tác dụng lên q 3 là F → = F 1 → + F 2 → . Để F → song song với AB thì F 2 → phải hướng về phía B tức là q 2 phải là điện tích âm và F 1 F 2 = A C B C (như hình vẽ).
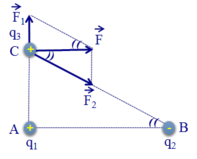
Vì F 1 = k | q 1 q 3 | A C 2 v à F 2 = k | q 2 q 3 | B C 2 ⇒ F 1 F 2 = | q 1 | B C 2 | q 2 | A C 2 = A C B C
⇒ q 2 = q 1 B C 3 A C 3 = 18 , 5 . 10 - 8 ( C ) . V ậ y q 2 = - 18 , 5 . 10 - 8 C .

a)vecto cường độ dòng diện do q1 và q2 gây ra tại C: phương trùng với cạnh AC,BC
b) lực điện từ tác dụng lên q3
A B C q1 q2 q3 F F 23 13
\(\overrightarrow{F_3}=\overrightarrow{F_{23}}+\overrightarrow{F_{13}}\)
theo độ lớn
\(F_3=\sqrt{F_{23}+F_{13}+2.F_{23}.F_{13}.cos\alpha}\)
ta có \(\alpha=180-60=120\)
r=0,03m
\(F_{23}=k.\frac{\left|q_2.q_3\right|}{\varepsilon.r^2}\) =.........N
\(F_{13}=k.\frac{\left|q_1.q_3\right|}{\varepsilon.r^2}\)=...........N
\(\Rightarrow F_3=..........N\)
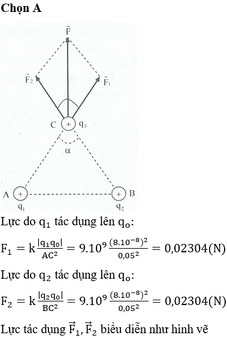

a. Xác định lực khi cho q1, q2 tác dụng lên q3
+ - - q1 q2 q3 F23 F13 A B C
Hợp lực tác dụng lên q3:
\(\vec{F_3}=\vec{F_{13}}+\vec{F_{23}}\)
Suy ra độ lớn:
\(F_3=F_{23}-F_{13}\) (1)
\(F_{13}=9.10^9.\dfrac{|q_1.q_3|}{AC^2}=9.10^9.\dfrac{|6.10^{-9}.2.10^{-9}|}{0,06^2}=3.10^{-5}N\)
\(F_{23}=9.10^9.\dfrac{|q_2.q_3|}{BC^2}=9.10^9.\dfrac{|3.10^{-9}.2.10^{-9}|}{0,03^2}=6.10^{-5}N\)
Thay vào (1) ta tìm được \(F_3=3.10^{-5}(N)\)
b. Ý này tương tự bạn nhé, phân tích lực --> Tổng hợp lực --> Rút ra biểu thức độ lớn --> Thay số.