Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

5C (công thức trong SGK, ko có gì cần tự luận ở đây)
6C: \(cos\left(a+\dfrac{\pi}{2}\right)=sin\left[\dfrac{\pi}{2}-\left(a+\dfrac{\pi}{2}\right)\right]=sin\left(-a\right)=-sina\)
7A: lý thuyết SGK, pt đường tròn có dạng \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\)
8A
Viết lại mẫu theo thứ tự và loại đi các mẫu lặp:
151 152 153 154 155 160 162 163 165 166 167
Từ đây ta thấy số trung vị là 160
9B: công thức định lý hàm cos trong SGK
10B (bấm máy)
11B (lý thuyết elip SGK)
12B (công thức lượng giác SGK)
13C.
Từ pt (E) ta thấy \(\left\{{}\begin{matrix}a^2=25\\b^2=24\end{matrix}\right.\) \(\Rightarrow c^2=a^2-b^2=1\Rightarrow c=1\)
Tiêu cự \(=2c=2\)
14D
\(\overline{t}=\dfrac{25+27+27+28+29+30+30+30+28+26+27+27}{12}\approx27,8\)
15D
\(\Leftrightarrow x^2+y^2-2x+\dfrac{5}{2}y-\dfrac{1}{2}=0\)
\(\Rightarrow I\left(1;-\dfrac{5}{4}\right)\)
16D (công thức SGK)

3.
Do \(sin\left(x+k2\pi\right)=sinx\Rightarrow sin\left(x+2020\pi\right)=sinx\)
\(sin\left(\dfrac{\pi}{2}+x\right)=cos\left(\dfrac{\pi}{2}-\dfrac{\pi}{2}-x\right)=cos\left(-x\right)=cosx\)
\(A=\dfrac{sinx+sin3x+sin5x}{cosx+cos3x+cos5x}=\dfrac{sinx+sin5x+sin3x}{cosx+cos5x+cos3x}\)
\(=\dfrac{2sin3x.cosx+sin3x}{2cos3x.cosx+cos3x}=\dfrac{sin3x\left(2cosx+1\right)}{cos3x\left(2cosx+1\right)}\)
\(=\dfrac{sin3x}{cos3x}=tan3x\)
4.
a.
\(\overrightarrow{CB}=\left(2;-2\right)=2\left(1;-1\right)\)
Do đường thẳng d vuông góc BC nên nhận \(\left(1;-1\right)\) là 1 vtpt
Phương trình đường thẳng d đi qua \(A\left(-1;2\right)\) và có 1 vtpt là \(\left(1;-1\right)\) là:
\(1\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow x-y+3=0\)
b.
Gọi \(I\left(a;b\right)\) là tâm đường tròn, ta có \(\left\{{}\begin{matrix}\overrightarrow{AI}=\left(a+1;b-2\right)\\\overrightarrow{BI}=\left(a-3;b-2\right)\\\overrightarrow{CI}=\left(a-1;b-4\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AI^2=\left(a+1\right)^2+\left(b-2\right)^2\\BI^2=\left(a-3\right)^2+\left(b-2\right)^2\\CI^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
Do I là tâm đường tròn qua 3 điểm nên: \(\left\{{}\begin{matrix}AI=BI\\AI=CI\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}AI^2=BI^2\\AI^2=CI^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a+1\right)^2+\left(b-2\right)^2=\left(a-3\right)^2+\left(b-2\right)^2\\\left(a+1\right)^2+\left(b-2\right)^2=\left(a-1\right)^2+\left(b-4\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8a=8\\4a+4b=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\) \(\Rightarrow I\left(1;2\right)\)
\(\overrightarrow{AI}=\left(2;0\right)\Rightarrow R=AI=\sqrt{2^2+0^2}=2\)
Pt đường tròn có dạng:
\(\left(x-1\right)^2+\left(y-2\right)^2=4\)

a) Bảng phân bố tần số (về tuổi thọ bóng đèn điện) có thể viết dưới dạng như sau:

Số trung bình về tuổi thọ của bóng đèn trong bảng phân bố trên là:
.(3x1150 + 6x1160 + 12x1170 + 6x1180 + 3x1190)
= 1170.
b) Số trung bình về chiều dài lá cây dương xỉ trong bài tập 2 trong là:
.(8x15 + 18x25 + 24x35 + 10x45) = 31 (cm).

a) Phương sai và độ lệch chuẩn trong bài tập 1. Bảng phân bố tần số viết lại là
![]()
Số trung bình: \(\overline{x} = 1170\)
Phương sai: \(S_{x}^{2}=\frac{1}{30}(3x1150^{2}+6x1160^{2}+12x1170^{2}+6x1180^{2}+3x1190^{2})-1170^{2} = 120\)
Độ lệch chuẩn: Sx.= \(\sqrt{S_{x}^{2}}=\sqrt{120} ≈ 10,9545\)
b) Phương sai và độ lệch chuẩn, bảng thống kê trong bài tập 2 \(\S 1.\)
\(S_{x}^{2}=\frac{1}{60}(8x15^{2}+18x25^{2}+24x35^{2}+10x45^{2}) - 312 = 84 \)
Sx ≈ 9,165.

a) Số trung bình điểm thi Ngữ văn của lớp 10C và 10D tương ứng là
.(3x5 + 7x6 + 12x7 + 14x8 + 3x9 + 1x10) = 7,25
.(8x6+18x7+10x8+4x9) = 7,25.
Phương sai bảng điểm thi Văn của hai lớp theo thứ tự là:
= 1,2875
= 0,7875.
Độ lệch chuẩn theo thứ tự là Sx ≈ 1,1347 Sy ≈ 0,8874.
b) Qua xem xét các số đặc trung ta thấy điểm trung bình thi văn 2 lớp 10C và 10D là như nhau (đều bằng 7,25). Nhưng phương sai của bảng điểm thi lớp 10D nhỏ hơn phương sai tương ứng ở lớp 10C. Điều đó chứng tỏ kết quả làm bài thi Văn ở lớp 10D đồng đều hơn.

a) Ta thấy đường thẳng \(y=ax+b\) đi qua hai điểm \(\left(0;3\right)\) và \(\left(1;0\right)\). Vậy ta có :
\(\left\{{}\begin{matrix}3=b\\0=a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=3\end{matrix}\right.\)
Đường thẳng có phương trình là \(y=-3x+3\)
b) \(y=-4x\)
c) \(y=x-2\)

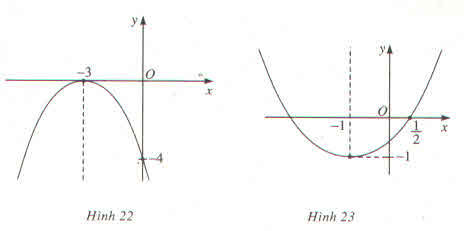
Hình 22
y=ax^2 +bx+c thỏa mãn hệ
\(\left\{{}\begin{matrix}y\left(0\right)=-4\Rightarrow c=-4\\y\left(-3\right)=9a-3b-4=0\\y\left(-6\right)=36a-6b-4=-4\end{matrix}\right.\)
(3) -(2) nhân 2
\(36a-18a-4+8=-4\Rightarrow18a=-8\Rightarrow a=\dfrac{-8}{18}=\dfrac{-4}{9}\)
Thế vào (2) -4-3b-4=0 => b=-8/3
Vậy pa ra bo; cho hình 22 là
\(y=-\dfrac{4}{9}x^2-\dfrac{8}{3}x-4\)

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.