
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các câu hỏi dưới đây có thể giống với câu hỏi trên

2 tháng 3 2017
Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)
Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)
Dấu \("="\) xảy ra khi:
\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)
Vậy \(1\le x\le5.\)
2 tháng 3 2017
Cho mk thêm cái ạ:
\(x\in\left\{1;2;3;4;5\right\}\)
Vậy \(x\in\left\{1;2;3;4;5\right\}\)

DN
12 tháng 5 2017
| Giá trị (x) | Tần số (n) | Các tích (x.n) | |
| 17 | 3 | 51 | |
| 18 | 5 | 90 | |
| 19 | 4 | 76 | |
| 20 | 2 | 40 | |
| 21 | 3 | 63 | |
| 22 | 2 | 44 | |
| 24 | 3 | 72 | |
| 26 | 3 | 78 | |
| 28 | 1 | 28 | |
| 30 | 1 | 30 | |
| 31 | 2 | 62 | |
| 32 | 1 | 32 | |
| N = 30 | Tổng: 666 |
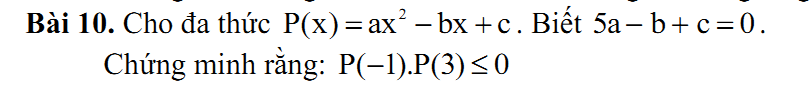














P(−1) = a + b + cP(3) = 9a − 3b + c
Lại có : 5a − b + c = 0⇒b = 5a + c
Thay b = 5a + c vào biểu thức P(-1) x P(3):
(a + 5a + c + c) x (9a − 15a − 3c + c)
=(6a + 2c) x (−6a − 2c)
=−(6a+2c^2
Và mình thấy là điều này khá là vô lý... Nên mình quyết định thử số xem sao.
Thử a = 1, b = 7 , c = 2.
Khi đó : P(-1) = 10 và P(3) = -10
Và P(-1) x P(3) thì .... lại không lớn hơn hoặc bằng 0?
Có thể đó là ≤≤chứ không phải ≥≥0?
Nếu đó là ≤≤, bạn có thể giải như trên.