Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo Cô si 4x+\frac{1}{4x}\ge24x+4x1≥2 , đẳng thức xảy ra khi và chỉ khi 4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}4x=4x1=1⇔x=41). Do đó
A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016A≥2−x+14x+3+2016
A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014A≥4−x+14x+3+2014
A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014A≥x+14x−4x+1+2014=x+1(2x−1)2+2014≥2014
Hơn nữa A=2014A=2014 khi và chỉ khi \left\{{}\begin{matrix}x=\dfrac{1}{4}\\2\sqrt{x}-1=0\end{matrix}\right.{x=412x−1=0 \Leftrightarrow x=\dfrac{1}{4}⇔x=41 .
Vậy GTNN = 2014

a: 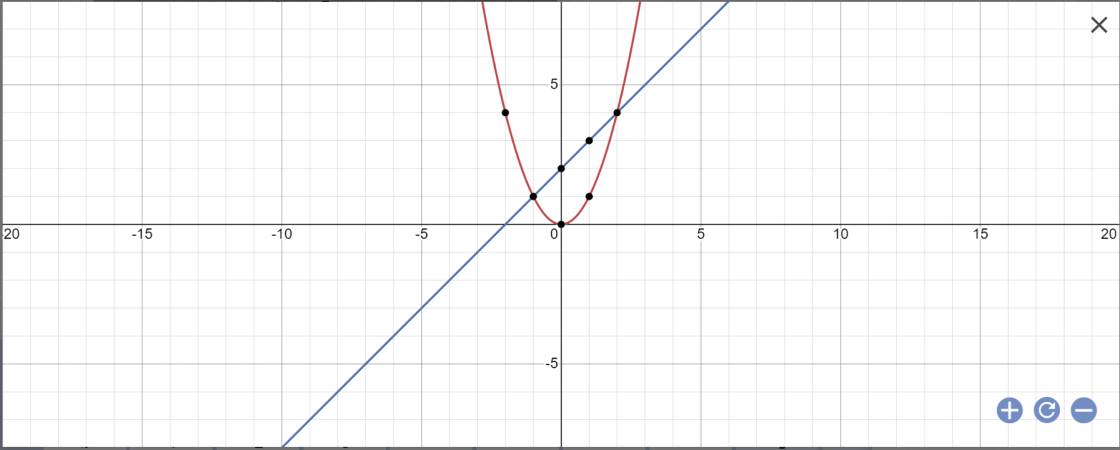
PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
Khi x=-1 thì y=(-1)^2=1
Khi x=2 thì y=2^2=4
b: Để y=(m-1)x+m+n trùng với y=-2x+1 thì
m-1=-2 và m+n=1
=>m=-1 và n=1-m=1-(-1)=2

Câu 1 bn tự làm nhé
2 .Thay x= \(\dfrac{-1}{2}vào\left(P\right)tađc:y=-2.\left(\dfrac{-1}{2}\right)^2=\dfrac{-1}{2}\)
Thay x=\(\dfrac{-1}{2}và\) y=\(\dfrac{-1}{2}\) vào (Dm) ta đc:
\(\dfrac{-1}{2}=-3.\left(\dfrac{-1}{2}\right)+m\)
=> m\(=-2\)
Vậy m=-2 thì (Dm ) cắt (P) tại điểm có hoành độ bằng -1/2
b) Pt hoành độ giao điểm của (P) y=-2x\(^2\) và ( Dm) y=-3x +m là
-2x\(^2\)=-3x +m => 2x\(^2\)-3x + m =0(1)
Ta có a= 2 ; b=-3 ; c=m
\(\Delta=b^2-4ac=\left(-3\right)^2-4.2.m=9-8m\)
Để (Dm) cắt (P) tại 2 điểm phân biệt \(\Leftrightarrow\Delta>0\Leftrightarrow9-8m>0\)
=>m < \(\dfrac{9}{8}\)
Vậy m<\(\dfrac{9}{8}thì\)(Dm) cắt (P) tại 2 điểm phân biệt
c) Để (Dm) tiếp xúc vs (P) \(\Leftrightarrow\Delta=0\Leftrightarrow9-8m=0=>m=\dfrac{9}{8}\)
Vậy m=9/8 thì (Dm) tiếp xúc vs (P)
Thay m=9/8 vào (1) ta dc : \(2x^2\)-3x+9/8=0
Ta có : a=2 ;b=-3 ;c=9/8
\(\Delta=b^2-4ac=\left(-3\right)^2-4.2.\dfrac{9}{8}=0\)
Vậy pt có nghiệm kép :
\(x_1=x_2=\dfrac{-b}{a}=\dfrac{3}{2}\)
Vs \(x_1=x_2=\dfrac{3}{2},\)\(\)ta có \(y_1=y_2=-2\left(\dfrac{3}{2}\right)^2=\dfrac{-9}{2}\)
Vậy tọa độ của tiếp điểm là ( 3/2 ; -9/2)

a: Thay x=0 và y=3 vào y=(m-1)x+m-5, ta được:
\(0\cdot\left(m-1\right)+m-5=3\)
=>m-5=3
=>m=8
b: Thay x=-1 và y=0 vào y=(m-1)x+m-5, ta được:
\(-\left(m-1\right)+m-5=0\)
=>-m+1+m-5=0
=>-4=0(vô lý)
c: Thay x=0 và y=0 vào y=(m-1)x+m-5, ta được:
\(0\left(m-1\right)+m-5=0\)
=>m-5=0
=>m=5

