
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 5b)
T = lx - 1l + lx + 2l + lx - 3l + lx + 4l + lx - 5l + lx + 6l + lx - 7l + lx + 8l + lx - 9l
Vì lx - 1l; lx + 2l; lx - 3l; lx + 4l; lx - 5l; lx + 6l; lx - 7l; lx + 8l; lx - 9l luôn \(\ge\)0 với mọi x
\(\Rightarrow\)lx - 1l + lx + 2l + lx - 3l + lx + 4l + lx - 5l + lx + 6l + lx - 7l + lx + 8l + lx - 9l\(\ge\)0 + 0 + 0 + .... + 0 = 0
\(\Rightarrow T\ge0\)với mọi x
\(\Rightarrow Min\)\(T=0\)\(\Leftrightarrow x\in\left\{1;-2;3;-4;5;-6;7;-8;9\right\}\)
Vậy giá trị nhỏ nhất của T = 0 \(khix\in\left\{1;-2;3;-4;5;-6;7;-8;9\right\}\)


\(\left(x-3\right).\left(x-2015\right)< 0\)
\(\Rightarrow\left(x-3\right)và\left(x-2015\right)\) phải khác dấu
\(\Rightarrow\left(x-3\right)< \left(x-2015\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-3>0\\x-2015< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>3\\x< 2015\end{matrix}\right.\)
\(\Rightarrow3< x< 2015\)
\(\Rightarrow x\in\left\{4;5;6;7;8;...;2013;2014\right\}\)
( ko bt đúng hay sai nx )
thám tử
\(\left(x-3\right)\left(x-2015\right)< 0\)
Với mọi \(x\in R\) thì:
\(x-2015< x-3\)
Khi đó: \(\left\{{}\begin{matrix}x-2015< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2015\\x>3\end{matrix}\right.\)
Nên \(3< x< 2015\)

\(a.\)
\(\Delta ABC\) cân tại \(A\Rightarrow\widehat{C}=\widehat{B}=55^0\)
Vậy \(\widehat{C}=55^0\)


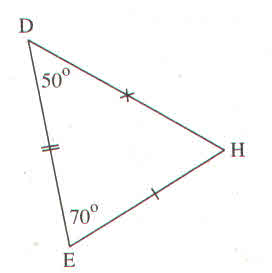



 Cho hình sau. Giải nhanh gọn lẹ giùm em do ko có time nên em ms chụp hình. Thoòng cảm giùm em
Cho hình sau. Giải nhanh gọn lẹ giùm em do ko có time nên em ms chụp hình. Thoòng cảm giùm em