Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ω = {(i, j, k) |1 ≤ i, j, k ≤ 6} gồm các chỉnh hợp chập 3 của 6 (số chấm).


Các biến cố thuận lợi (1;6);(6;1);(2;5);(5;2);(3;4);(4;3) có 6 phần tử

a. Có 3 mặt nguyên tố: 2,3,5 nên xác suất xuất hiện số nguyên tố ở mỗi lần gieo là \(\dfrac{3}{6}=\dfrac{1}{2}\)
Xác suất 2 lần đều xuất hiện số nguyên tố: \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)
b. Xác suất để lần 1 xuất hiện mặt 6 chấm: \(\dfrac{1}{6}\)
c. Xác suất ít nhất 1 lần xuất hiện mặt 6 chấm: \(\dfrac{2.6-1}{36}=\dfrac{11}{36}\)
d. Xác suất ko lần nào xuất hiện 6 chấm: \(1-\dfrac{11}{36}=\dfrac{25}{36}\)

Không gian mẫu là tập hợp số chấm xuất hiện khi gieo con xúc xắc hai lần liên tiếp khi đó \(n\left( \Omega \right) = 6.6 = 36\)
A = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6)} \( \Rightarrow P\left( A \right) = \frac{6}{{36}} = \frac{1}{6}\)
B = {(1; 2); (2; 2); (3; 2); (4; 2); (5; 2); (6; 2)} \( \Rightarrow P\left( B \right) = \frac{6}{{36}} = \frac{1}{6}\)
C = {(2; 6); (3; 5); (4; 4); (5; 3); (6; 2)} \( \Rightarrow P\left( C \right) = \frac{5}{{36}}\)
D = {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)} \( \Rightarrow P\left( D \right) = \frac{6}{{36}} = \frac{1}{6}\)
Do đó
\(P\left( A \right).P\left( C \right) = \frac{1}{6}.\frac{5}{{36}} = \frac{5}{{216}};P\left( B \right).P\left( C \right) = \frac{1}{6}.\frac{5}{{36}} = \frac{5}{{216}};P\left( C \right).P\left( D \right) = \frac{5}{{36}}.\frac{1}{6} = \frac{5}{{216}}\)
Mặt khác
AC = \(\emptyset \Rightarrow P\left( {AC} \right) = 0\)
BC = {(6; 2)} \( \Rightarrow P\left( {BC} \right) = \frac{1}{{36}}\)
CD = \(\emptyset \Rightarrow P\left( {CD} \right) = 0\)
Khi đó \(P\left( {AC} \right) \ne P\left( A \right).P\left( C \right);P\left( {BC} \right) \ne P\left( B \right).P\left( C \right);P\left( {CD} \right) \ne P\left( C \right).P\left( D \right)\)
Vậy các cặp biến cố A và C; B và C, C và D không độc lập.

Đây giống với xác suất đại học hơn thì phải, cấp 3 hình như người ta ko cho dạng này (công thức Bernoulli)
\(P=C_4^1.\left(\dfrac{1}{6}\right)^1.\left(\dfrac{5}{6}\right)^{4-1}\)

a. Không gian mẫu gồm 36 kết quả đồng khả năng xuất hiện, được mô tả như sau:
Ta có: Ω = {(i, j) | 1 ≤ i , j ≤ 6}, trong đó i, j lần lượt là số chấm xuất hiện trong lần gieo thứ nhất và thứ hai, n(Ω) = 36.
b. A = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)} ⇒ n(A) = 6
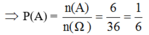
B = {(1, 5), (2, 5), (3, 5), (4, 5), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 5)}
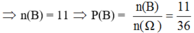

Gọi A i là biến cố “ mặt 4 chấm xuất hiện lần thứ i” với i = 1; 2; 3; 4.
Khi đó: A i là biến cố “ Mặt 4 chấm không xuất hiện lần thứ i”
Và P ( A i ¯ ) = 1 − P ( A i ) = 1 − 1 6 = 5 6
Ta có: A ¯ là biến cố: “ không có mặt 4 chấm xuất hiện trong 4 lần gieo”
Và A ¯ = A 1 ¯ . A 2 ¯ . A 3 ¯ . A 4 ¯ . Vì các A i ¯ độc lập với nhau nên ta có:
P ( A ¯ ) = P ( A 1 ¯ ) . P ( A 2 ¯ ) . P ( A 3 ¯ ) . P ( A 4 ¯ ) = 5 6 4
Vậy P ( A ) = 1 − P ( A ¯ ) = 1 − 5 6 4 .
Chọn đáp án A.
