Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có thể là 2 lần chẵn 1 lần lẻ hoặc cả 3 lần đều chẵn
TH1: 2 chẵn, 1 lẻ
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
TH2: 3 lần đều chẵn
=>Có \(C^1_3\cdot C^1_3\cdot C^1_3=27\left(cách\right)\)
=>Có 27+27=54 cách
n(omega)=6*6*6=216
=>P=54/216=1/4

a: A={(1;1); (1;2); ...; (1;6)}
=>n(A)=6
P(A)=6/36=1/6
b: B={(1;4); (2;3); (3;2); (4;1)}
=>P(B)=4/36=1/9
c: C={(3;1); (4;2); (5;3); (6;4)}
=>P(C)=4/36=1/9
d: D={(1;3); (1;5); (1;1); (3;5); (3;1); (3;3); (5;3); (5;1); (5;5)}
=>P(D)=9/36=1/4

Câu 1: Gieo 1 đồng tiền cân đối và đồng chất 2 lần
\(\Rightarrow n\left(\Omega\right)=2^2=4\)
Gọi A là biến cố cả hai lần xuất hiện mặt sấp
\(\Rightarrow A=\left\{SS\right\}\Rightarrow n\left(A\right)=1\)
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{1}{4}\)
Chọn B
Câu 2: Số phần tử không gian mẫu: \(n\left(\Omega\right)=6\)
Gọi biến cố A: “Số chấm là số nguyên tố xuất hiện”
\(A=\left\{2;3;5\right\}\)
\(\Rightarrow n\left(A\right)=3\)
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{3}{6}=\dfrac{1}{2}\)
Chọn A

A={(1;2); (1;5); (2;4); (2;1); (3;3); (3;6); (4;2); (4;5); (5;1); (5;4); (6;3); (6;6)}
=>n(A)=12
n(omega)=36
=>P(A)=12/36=1/3

+) Không gian mẫu trong trò chơi trên là tập hợp \(\Omega = {\rm{ }}\left\{ {\left( {i,j} \right){\rm{ | }}i,{\rm{ }}j{\rm{ }} = {\rm{ }}1,{\rm{ }}2,{\rm{ }}3,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6} \right\}\) trong đó (i,j) là kết quả “Lần thứ nhất xuất hiện mặt i chấm, lần thứ hai xuất hiện mặt j chấm”. Vậy \(n\left( \Omega \right) = 36\)
+) Gọi A là biến cố “Số chấm trong hai lần gieo đều là số nguyên tố”.
Ta có các kết quả thuận lợi cho biến cố A là: (2 ; 2) (2;3) (2;5) (3; 2) (3;3) (3;5) (5;2) (5;3) (5;5). Vậy \(n\left( A \right) = 9\)
+) Vậy xác suất của biến cố A là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{9}{{36}} = \frac{1}{4}\)

a) Kí hiệu S là đồng xu ra mặt sấp và N là đồng xu ra mặt ngửa. Ta có sơ đồ cây
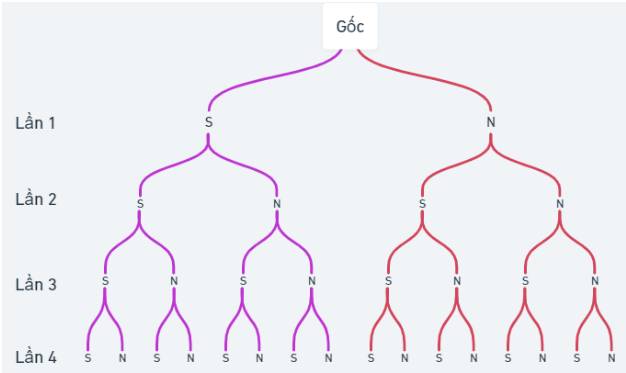
Dựa vào sơ đồ cây ta suy ra \(n\left( \Omega \right) = 16\).
b) Gọi A là biến cố: “gieo đồng xu 4 lần có hai lần xuất hiện mặt sấp và hai lần xuất hiện mặt ngửa”
Suy ra \(A = \left\{ {SSNN;SNSN;SNNS;NSSN;NSNS;NNSS} \right\}\). Suy ra \(n\left( A \right) = 6\). Vậy\(P\left( A \right) = \frac{6}{{16}} = \frac{3}{8}\).

n(omega)=2*2*2=8
A={(NNS); (NSN); (SNN)}
=>n(A)=3
=>P(A)=3/8

Không gian mẫu trong trò chơi trên là tập hợp \(\Omega = \left\{ {(i,j)|i,j = 1,2,3,4,5,6} \right\}\)trong đó (i,j) là kết quả “Lần thứ nhất xuất hiện mặt i chấm, lần thứ hai xuất hiện mặt j chấm”. Vậy \(n(\Omega ) = \;36.\)
a) Gọi A là biến cố “Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10”.
Các kết quả có lợi cho A là: (4; 6) (5;5) (5;6) (6; 4) (6;5) (6;6). Vậy \(n(A) = \;6.\)
Vậy xác suất của biến cố A là \(P(A) = \;\frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{36}} = \frac{1}{6}.\)
b) Gọi B là biến cố “Mặt 1 chấm xuất hiện ít nhất một lần”.
Các kết quả có lợi cho B là: (1; 1) (1 : 2) (1 : 3) (1; 4) (1;5) (1; 6) (2 ; 1) (3;1) (4; 1) (5;1) (6;1). Vậy \(n(B) = \;11.\)
Vậy xác suất của biến cố B là: \(P(B) = \;\frac{{n(B)}}{{n(\Omega )}} = \frac{{11}}{{36}}.\)
n(omega)=6*6=36
n(A)=6
=>P(A)=6/36=1/6