Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo:
Nếu \(lim\) (x->1) \(\dfrac{f\left(x\right)-5}{x-1}=2\) và lim (x->1) \(\dfrac{g\left(x\right)-1}{x-1}=3\) thì lim (x->1... - Hoc24
Không giống hoàn toàn, nhưng cách làm thì giống hoàn toàn

\(\lim\limits_{x\rightarrow3}f\left(x\right)=\lim\limits_{x\rightarrow3}\frac{8x^{2016}-24x^{2015}}{x^{2017}+2x^{2016}-15x^{2015}}=\lim\limits_{x\rightarrow3}\frac{8\left(x-3\right)}{x^2+2x-15}=\lim\limits_{x\rightarrow3}\frac{8\left(x-3\right)}{\left(x-3\right)\left(x+5\right)}=\lim\limits_{x\rightarrow3}\frac{8}{x+5}=1\)
\(\lim\limits_{x\rightarrow1}g\left(x\right)=\lim\limits_{x\rightarrow1}\frac{\sqrt{2x+2}-2+2-\sqrt{3x+1}}{m\left(x-1\right)\left(x+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{\frac{2\left(x-1\right)}{\sqrt{2x+2}+2}-\frac{3\left(x-1\right)}{2+\sqrt{3x+1}}}{m\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1}\frac{\frac{2}{\sqrt{2x+2}+2}-\frac{3}{2+\sqrt{3x+1}}}{m\left(x+1\right)}=\frac{\frac{2}{4}-\frac{3}{4}}{2m}=-\frac{1}{8m}\)
\(\Rightarrow-\frac{1}{8m}=1\Rightarrow m=-\frac{1}{8}\)

\(A=\lim\limits_{x\rightarrow2}\frac{\left(x-2\right)\left(2x-1\right)}{x-2}=\lim\limits_{x\rightarrow2}\left(2x-1\right)=3\)
\(B=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x^2-2x+3\right)}{\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1}\frac{x^2-2x+3}{x+1}=\frac{1-2+3}{1+1}=1\)
\(C=\lim\limits_{x\rightarrow2}\frac{x^2+2x}{x^2+4x+4}=\frac{4+4}{4+8+4}=\frac{1}{2}\)
\(D=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x^2-1\right)}{\left(x-1\right)\left(x-2\right)}=\lim\limits_{x\rightarrow1}\frac{x^2-1}{x-2}=\frac{0}{-1}=0\)
\(E=\lim\limits_{x\rightarrow1}\frac{x^3-5x^2+3x+9}{x^4-8x^4-9}=\frac{1-5+3+9}{1-8-9}=-\frac{1}{2}\)
\(F=\lim\limits_{x\rightarrow-1}\frac{\left(x+1\right)\left(x-1\right)\left(x^2+1\right)}{\left(x+1\right)\left(x^2-3x+3\right)}=\lim\limits_{x\rightarrow-1}\frac{\left(x-1\right)\left(x^2+1\right)}{x^2-3x+3}=\frac{-2.2}{1+3+3}=-\frac{2}{5}\)
\(G=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x+3\right)}{\left(x-1\right)\left(2x+1\right)}=\lim\limits_{x\rightarrow1}\frac{x+3}{2x+1}=\frac{4}{3}\)
\(H=\lim\limits_{x\rightarrow-2}\frac{\left(x+2\right)\left(x-1\right)^2}{\left(2-x\right)\left(x+2\right)}=\lim\limits_{x\rightarrow-2}\frac{\left(x-1\right)^2}{2-x}=\frac{9}{4}\)
\(I=\lim\limits_{x\rightarrow1}\frac{4x^6-5x^5+1}{x^2-1}=\lim\limits_{x\rightarrow1}\frac{24x^5-25x^4}{2x}=\frac{24-25}{2}=-\frac{1}{2}\)
\(K=\lim\limits_{x\rightarrow1}\frac{x^m-1}{x^n-1}=\lim\limits_{x\rightarrow1}\frac{mx^{m-1}}{nx^{n-1}}=\frac{m}{n}\)

Do \(x-1\rightarrow0\) khi \(x\rightarrow1\) nên \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-5}{x-1}=2\) hữu hạn khi và chỉ khi \(f\left(x\right)-5=0\) có nghiệm \(x=1\)
\(\Leftrightarrow f\left(1\right)-5=0\Rightarrow f\left(1\right)=5\)
Tương tự ta có \(g\left(1\right)=1\)
Do đó: \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{f\left(x\right).g\left(x\right)+4}-3}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right).g\left(x\right)-5}{\left(x-1\right)\left(\sqrt{f\left(x\right).g\left(x\right)+4}+3\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left[f\left(x\right)-5\right].g\left(x\right)+5\left[g\left(x\right)-1\right]}{\left(x-1\right)\left(\sqrt{f\left(x\right).g\left(x\right)+4}+3\right)}\)
\(=\left(2.1+5.3\right).\dfrac{1}{\sqrt{5.1+4}+3}=\dfrac{17}{6}\)
Em làm như này được ko anh?
Tìm lim f(x) theo lim của x, rồi thế vô biểu thức, ví dụ như: \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-5}{x-1}=2\Rightarrow\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\left[2\left(x-1\right)+5\right]\)
Vậy là mình có thể chuyển từ tìm lim f(x) sang lim của hàm số chứa x


Đề là \(\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-5}{x-3}\) hay \(\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-15}{x-3}\) em?
\(\dfrac{f\left(x\right)-5}{x-3}\) thì giới hạn bên dưới ko phải dạng vô định, kết quả là vô cực
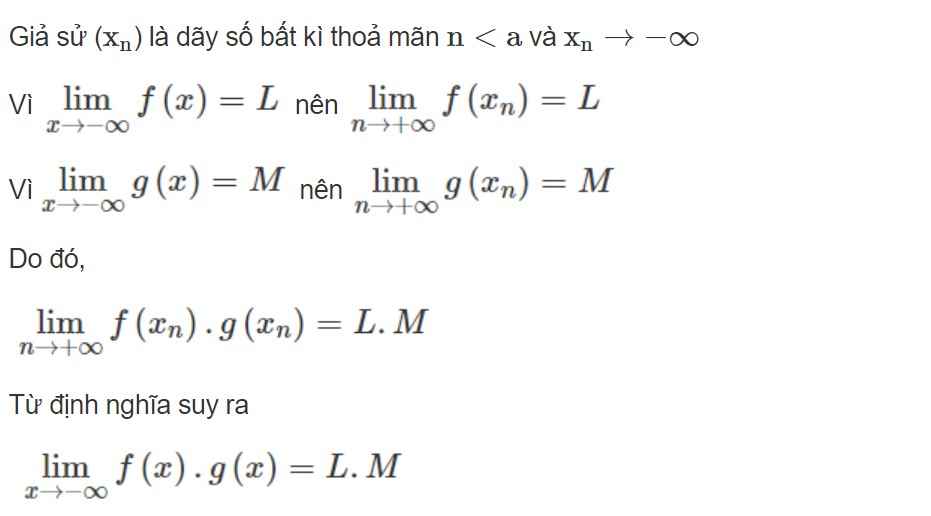
Lời giải:
Theo định nghĩa về giới hạn thì khi \(\lim_{x\to -\infty}f(x)=2; \lim_{x\to -\infty}g(x)=3\) thì \(\lim_{x\to -\infty}[f(x)-2]=0; \lim_{x\to -\infty}[g(x)-3]=0\)
Khi đó, theo định nghĩa về giới hạn 0 thì với mọi số \(\epsilon >0\) ta tìm được tương ứng $n_1,n_2$ sao cho:
\(\left\{\begin{matrix} |f(x)-2|<\frac{\epsilon}{2}\forall n>n_1\\ |g(x)-3|< \frac{\epsilon}{2}\forall n>n_2\end{matrix}\right.\)
Gọi \(n_0=\max (n_1,n_2)\)
\(\Rightarrow |f(x)-2+g(x)-3|< |f(x)-2|+|g(x)-3|< \frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon \) \(\forall n>n_0\)
Điều này chứng tỏ \(f(x)-2+g(x)-3=f(x)+g(x)-5\) có giới hạn 0
\(\Rightarrow \lim_{x\to -\infty}[f(x)+g(x)]=5\)