Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+4x}.\sqrt[3]{1+6x}.\sqrt[4]{1+8x}-\sqrt[3]{1+6x}.\sqrt[4]{1+8x}}{x}+\lim\limits_{x\rightarrow0}\dfrac{\sqrt[3]{1+6x}.\sqrt[4]{1+8x}-\sqrt[3]{1+6x}}{x}+\lim\limits_{x\rightarrow0}\dfrac{\sqrt[3]{1+6x}-1}{x}\)
Liên hợp dài quá ko muốn gõ tiếp, bạn tự đặt nhân tử chung rồi liên hợp nhé, kết quả ra 5
2/ \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{1+7x}-2-\left(x^3-3x+2\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{7\left(x-1\right)}{\sqrt[3]{\left(1+7x\right)^2}+2\sqrt[3]{1+7x}+4}-\left(x-1\right)^2\left(x+2\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{7}{\sqrt[3]{\left(1+7x\right)^2}+2\sqrt[3]{1+7x}+4}-\left(x-1\right)\left(x+2\right)=\dfrac{7}{12}\)
3/ \(\lim\limits_{x\rightarrow-\infty}\dfrac{x^3-x^2+1}{2x^2+3x-1}=\lim\limits_{x\rightarrow-\infty}\dfrac{x-1+\dfrac{1}{x^2}}{2+\dfrac{3}{x}-\dfrac{1}{x^2}}=-\infty\)
4/ \(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x}+\sqrt[3]{x}+\sqrt[4]{x}}{\sqrt{4x+1}}=\lim\limits_{x\rightarrow+\infty}\dfrac{1+\dfrac{1}{\sqrt[6]{x}}+\dfrac{1}{\sqrt[4]{x}}}{\sqrt{4+\dfrac{1}{x}}}=\dfrac{1}{\sqrt{4}}=\dfrac{1}{2}\)
5/ \(\lim\limits_{x\rightarrow-\infty}\dfrac{x+\sqrt{x^2+2}}{\sqrt[3]{8x^3+x^2+1}}=\lim\limits_{x\rightarrow-\infty}\dfrac{1-\sqrt{1+\dfrac{2}{x^2}}}{\sqrt[3]{8+\dfrac{1}{x}+\dfrac{1}{x^3}}}=\dfrac{1-1}{\sqrt[3]{8}}=0\)
6/ \(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{4x^2+3x-7}}{\sqrt[3]{27x^3+5x^2+x-4}}=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{4+\dfrac{3}{x}-\dfrac{7}{x^2}}}{\sqrt[3]{27+\dfrac{5}{x}+\dfrac{1}{x^2}-\dfrac{4}{x^3}}}=\dfrac{-\sqrt{4}}{\sqrt[3]{27}}=\dfrac{-2}{3}\)

1/ \(\lim\limits_{x\rightarrow0}\dfrac{2\sqrt{1+x}-2+2-\sqrt[3]{8-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{2x}{\sqrt{1+x}+1}+\dfrac{x}{4+2\sqrt[3]{8-x}+\sqrt[3]{\left(8-x\right)^2}}}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(\dfrac{2}{\sqrt{1+x}+1}+\dfrac{1}{4+2\sqrt[3]{8-x}+\sqrt[3]{\left(8-x\right)^2}}\right)=\dfrac{13}{12}\)
2/ \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x+7}-\sqrt{x+3}}{x^2-3x+2}=\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x+7}-2-\left(\sqrt{x+3}-2\right)}{\left(x-1\right)\left(x-2\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{x-1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}-\dfrac{x-1}{\sqrt{x+3}+2}}{\left(x-1\right)\left(x-2\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{1}{\sqrt[3]{\left(x+7\right)^2}+2\sqrt[3]{x+7}+4}-\dfrac{1}{\sqrt{x+3}+2}}{x-2}=\dfrac{1}{6}\)
3/ \(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x^2+7}-\sqrt{5-x^2}}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x^2+7}-2+2-\sqrt{5-x^2}}{x^2-1}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{\left(x^2-1\right)}{\sqrt[3]{\left(x^2+7\right)^2}+2\sqrt[3]{x^2+7}+4}+\dfrac{x^2-1}{2+\sqrt{5-x^2}}}{x^2-1}\)
\(=\lim\limits_{x\rightarrow1}\left(\dfrac{1}{\sqrt[3]{\left(x^2+7\right)^2}+2\sqrt[3]{x^2+7}+4}+\dfrac{1}{2+\sqrt{5-x^2}}\right)=\dfrac{1}{3}\)
4/ \(\lim\limits_{x\rightarrow-2}\dfrac{\sqrt{x+11}-\sqrt[3]{8x+43}}{2x^2+3x-2}=\lim\limits_{x\rightarrow-2}\dfrac{\sqrt{x+11}-3-\left(\sqrt[3]{8x+43}-3\right)}{\left(2x-1\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow-2}\dfrac{\dfrac{x+2}{\sqrt{x+11}+3}-\dfrac{8\left(x+2\right)}{\sqrt[3]{\left(8x+43\right)^2}+3\sqrt[3]{8x+43}+9}}{\left(2x-1\right)\left(x+2\right)}\)
\(=\lim\limits_{x\rightarrow-2}\dfrac{\dfrac{1}{\sqrt{x+11}+3}-\dfrac{8}{\sqrt[3]{\left(8x+43\right)^2}+3\sqrt[3]{8x+43}+9}}{2x-1}=\dfrac{7}{270}\)
5/ \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt[n]{1+ax}-\sqrt[m]{1+bx}}{x}=\lim\limits_{x\rightarrow0}\dfrac{\sqrt[n]{1+ax}-1-\left(\sqrt[m]{1+bx}-1\right)}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\dfrac{ax}{\sqrt[n]{\left(1+ax\right)^{n-1}}+\sqrt[n]{\left(1+ax\right)^{n-2}}+...+1}-\dfrac{bx}{\sqrt[m]{\left(1+bx\right)^{m-1}}+\sqrt[m]{\left(1+ax\right)^{m-2}}+...+1}}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{a}{\sqrt[n]{\left(1+ax\right)^{n-1}}+\sqrt[n]{\left(1+ax\right)^{n-2}}+...+1}-\dfrac{b}{\sqrt[m]{\left(1+bx\right)^{m-1}}+\sqrt[m]{\left(1+ax\right)^{m-2}}+...+1}\)
\(=\dfrac{a}{n}-\dfrac{b}{m}\)
6/ \(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+4x}.\sqrt[3]{1+6x}-1}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+4x}.\sqrt[3]{1+6x}-\sqrt{1+4x}+\sqrt{1+4x}-1}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+4x}.\left(\sqrt[3]{1+6x}-1\right)+\sqrt{1+4x}-1}{x}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+4x}.\dfrac{6x}{\sqrt[3]{\left(1+6x\right)^2}+\sqrt[3]{1+6x}+1}+\dfrac{4x}{\sqrt{1+4x}+1}}{x}\)
\(=\lim\limits_{x\rightarrow0}\left(\dfrac{6\sqrt{1+4x}}{\sqrt[3]{\left(1+6x\right)^2}+\sqrt[3]{1+6x}+1}+\dfrac{4}{\sqrt{1+4x}+1}\right)=4\)

3.3 d)
\(\sin8x-\cos6x=\sqrt{3}\left(\sin6x+\cos8x\right)\\ \Leftrightarrow\sin8x-\sqrt{3}\cos8x=\sqrt{3}\sin6x+\cos6x\\ \Leftrightarrow\sin\left(8x-\dfrac{\pi}{3}\right)=\sin\left(6x+\dfrac{\pi}{6}\right)\\ \Leftrightarrow\left[{}\begin{matrix}8x-\dfrac{\pi}{3}=6x+\dfrac{\pi}{6}+k2\pi\\8x-\dfrac{\pi}{3}=\pi-\left(6x+\dfrac{\pi}{6}\right)+k2\pi\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{12}+k\dfrac{\pi}{7}\end{matrix}\right.\)
3.4 a)
\(2sin\left(x+\dfrac{\pi}{4}\right)+4sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{3\sqrt{2}}{5}\\ \Leftrightarrow2cos\left(\dfrac{\pi}{2}-x-\dfrac{\pi}{4}\right)+4sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{3\sqrt{2}}{5}\\ \Leftrightarrow2cos\left(-x+\dfrac{\pi}{4}\right)+4sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{3\sqrt{2}}{5}\\ \Leftrightarrow2cos\left(x-\dfrac{\pi}{4}\right)+4sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{3\sqrt{2}}{5}\\ \)
Chia hai vế cho \(\sqrt{2^2+4^2}=2\sqrt{5}\)
Ta được:
\(\dfrac{1}{\sqrt{5}}cos\left(x-\dfrac{\pi}{4}\right)+\dfrac{2}{\sqrt{5}}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{3}{4}\\ \)
Gọi \(\alpha\) là góc có \(cos\alpha=\dfrac{1}{\sqrt{5}}\)và \(sin\alpha=\dfrac{2}{\sqrt{5}}\)
Phương trình tương đương:
\(cos\left(x-\dfrac{\pi}{4}-\alpha\right)=\dfrac{3}{4}\\ \Leftrightarrow x=\pm arscos\left(\dfrac{3}{4}\right)+\dfrac{\pi}{4}+\alpha+k2\pi\)

1.
\(\lim\limits_{x\to (-1)-}\frac{\sqrt{x^2-3x-4}}{1-x^2}=\lim\limits_{x\to (-1)-}\frac{\sqrt{(x+1)(x-4)}}{(1-x)(1+x)}\)
\(=\lim\limits_{x\to (-1)-}\frac{\sqrt{4-x}}{(x-1)\sqrt{-(x+1)}}=-\infty\) do:
\(\lim\limits_{x\to (-1)-}\frac{\sqrt{4-x}}{x-1}=\frac{-\sqrt{5}}{2}<0\) và \(\lim\limits_{x\to (-1)-}\frac{1}{\sqrt{-(x+1)}}=+\infty\)
2.
\(\lim\limits_{x\to 2+}\left(\frac{1}{x-2}-\frac{x+1}{\sqrt{x+2}-2}\right)=\lim\limits_{x\to 2+}\frac{1-(x+1)(\sqrt{x+2}+2)}{x-2}=-\infty\) do:
\(\lim\limits_{x\to 2+}\frac{1}{x-2}=+\infty\) và \(\lim\limits_{x\to 2+}[1-(x+1)(\sqrt{x+2}+2)]=-11<0\)
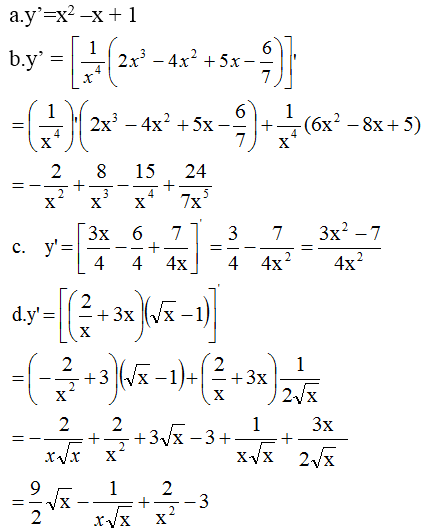
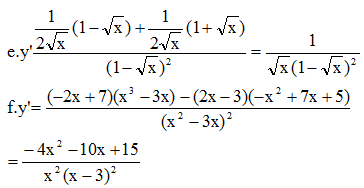


a.
\(\Leftrightarrow4x^2-6x+1+\dfrac{1}{\sqrt{3}}\sqrt{\left(4x^2-2x+1\right)\left(4x^2+2x+1\right)}\)
Đặt \(\left\{{}\begin{matrix}\sqrt{4x^2-2x+1}=a>0\\\sqrt{4x^2+2x+1}=b>0\end{matrix}\right.\) ta được:
\(2a^2-b^2+\dfrac{1}{\sqrt{3}}ab=0\)
\(\Leftrightarrow\left(a-\dfrac{b}{\sqrt{3}}\right)\left(2a+\sqrt{3}b\right)=0\)
\(\Leftrightarrow a=\dfrac{b}{\sqrt{3}}\)
\(\Leftrightarrow3a^2=b^2\)
\(\Leftrightarrow3\left(4x^2-2x+1\right)=4x^2+2x+1\)
\(\Leftrightarrow...\)
b.
\(x^2-3x+1+\dfrac{1}{\sqrt{3}}\sqrt{\left(x^2-x+1\right)\left(x^2+x+1\right)}\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x^2-x+1}=a>0\\\sqrt{x^2+x+1}=b>0\end{matrix}\right.\)
\(\Rightarrow2a^2-b^2+\dfrac{1}{\sqrt{3}}ab=0\)
Lặp lại cách làm câu a