K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
17 tháng 5 2017
\(4\sin3x+\sin5x-2\sin x\cos2x=0\)
\(\Leftrightarrow\)\(4\sin3x+\sin5x-\sin3x+\sin x=0\)
\(\Leftrightarrow3\sin3x+\sin5x+\sin x=0\)
\(\Leftrightarrow3\sin3x+2\sin3x\cos2x=0\)
\(\Leftrightarrow\sin3x\left(3+2\cos2x\right)=0\)
Đáp số : \(x=k\dfrac{\pi}{3},k\in\mathbb{Z}\)
TN
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 10 2019
\(\Leftrightarrow\sqrt{3}cos5x-\left(sin5x+sinx\right)-sinx=0\)
\(\Leftrightarrow\sqrt{3}cos5x-sin5x=2sinx\)
\(\Leftrightarrow\frac{\sqrt{3}}{2}cos5x-\frac{1}{2}sin5x=sinx\)
\(\Leftrightarrow sin\left(\frac{\pi}{3}-5x\right)=sinx\)
\(\Leftrightarrow...\)
3 tháng 4 2017
a) cosx - √3sinx = √2 ⇔ cosx - tan
sinx = √2
⇔ coscosx - sinsinx = √2cos ⇔ cos(x + ) = 
⇔ 
3 tháng 4 2017
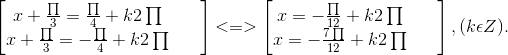
b) 3sin3x - 4cos3x = 5 ⇔ 
sin3x - 
cos3x = 1.
Đặt α = arccos thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = 
+ k2π
⇔ x = 
, k ∈ Z (trong đó α = arccos).
TN
0
29 tháng 9 2020
a.\(\frac{k\Pi}{2}+\frac{\alpha}{2}\)
b.\(\left\{{}\begin{matrix}x=\frac{1}{4}arcsin\left(\frac{1}{3}\right)+\frac{k\Pi}{2}-\frac{1}{8}\\x=\Pi-\frac{1}{4}arcsin\left(\frac{1}{3}\right)+\frac{k\Pi}{2}-\frac{1}{8}\end{matrix}\right.\)
\(sin3x-4sinx\cdot cos2x=0\\ \Leftrightarrow3sinx-4sin^3x-4sinx\left(1-2sin^2x\right)=0\Leftrightarrow4sin^3x-sinx=0\\ \Leftrightarrow\left[{}\begin{matrix}sinx=0\\2sin^2x=\frac{1}{2}\end{matrix}\right.\Leftrightarrow}\left[{}\begin{matrix}x=k\pi\\x=\pm\frac{\pi}{6}+n\pi\end{matrix}\right.\)