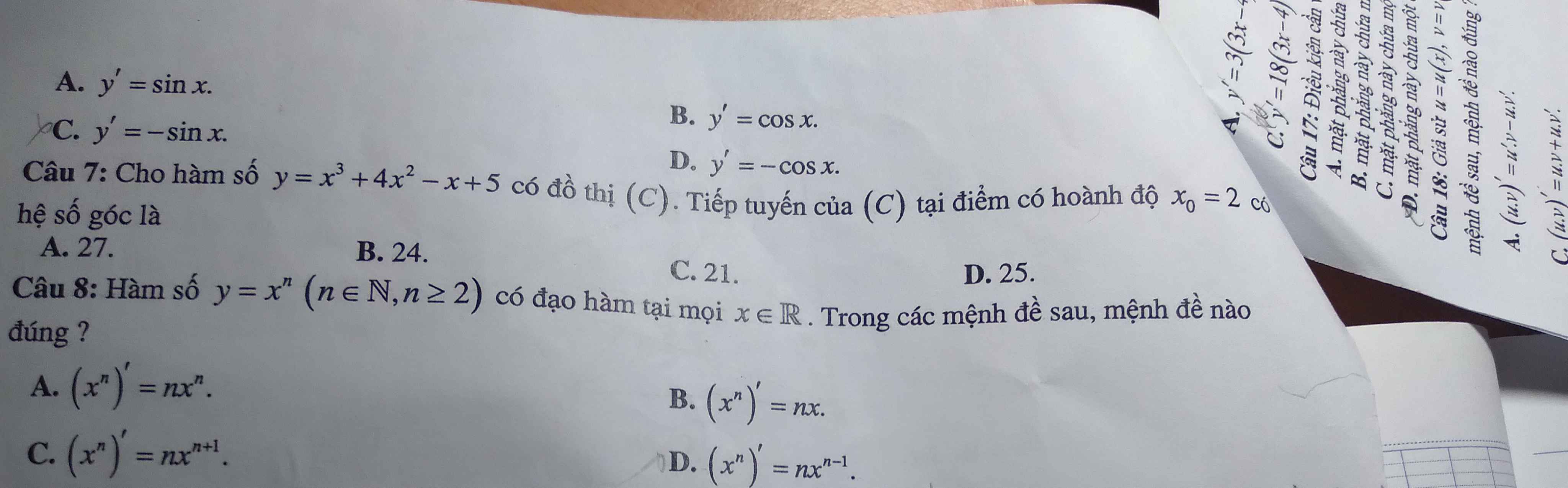Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Ta có : \(SA\perp\left(ABCD\right)\Rightarrow BC\perp SA\)
Đáy ABCD là HV \(\Rightarrow BC\perp AB\)
Suy ra : \(BC\perp\left(SAB\right)\Rightarrow\left(SAB\right)\perp\left(SBC\right)\) ( đpcm )
b. \(\left(SBD\right)\cap\left(ABCD\right)=BD\)
O = \(AC\cap BD\) ; ta có : \(AO\perp BD;AO=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{2}a\)
Dễ dàng c/m : \(BD\perp\left(SAC\right)\) \(\Rightarrow SO\perp BD\)
Suy ra : \(\left(\left(SBD\right);\left(ABCD\right)\right)=\left(SO;AO\right)=\widehat{SOA}\)
\(\Delta SAO\perp\) tại A có : tan \(\widehat{SOA}=\dfrac{SA}{AO}=\dfrac{a}{\dfrac{\sqrt{2}}{2}a}=\sqrt{2}\)
\(\Rightarrow\widehat{SOA}\approx54,7^o\) \(\Rightarrow\) ...

a.
\(\Leftrightarrow\left(sinx+cosx\right)\left(1+sinx.cosx\right)=1\)
Đặt \(sinx+cosx=t\) \(\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=1+2sinx.cosx\Rightarrow sinx.cosx=\dfrac{t^2-1}{2}\)
Phương trình trở thành:
\(t\left(1+\dfrac{t^2-1}{2}\right)=1\)
\(\Leftrightarrow t^3+t-2=0\)
\(\Leftrightarrow\left(t-1\right)\left(t^2+t+2\right)=0\)
\(\Leftrightarrow t=1\)
\(\Rightarrow sinx+cosx=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}=sin\left(\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow...\)
b.
Đặt \(sinx-cosx=t\Rightarrow-\sqrt{2}\le t\le\sqrt{2}\)
\(t^2=1-2sinx.cosx\Rightarrow sinx.cosx=\dfrac{1-t^2}{2}\)
Phương trình trở thành:
\(t^3=1+\dfrac{1-t^2}{2}\)
\(\Leftrightarrow2t^3+t^2-3=0\)
\(\Leftrightarrow\left(t-1\right)\left(2t^2+3t+3\right)=0\)
\(\Leftrightarrow t=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}=sin\left(\dfrac{\pi}{4}\right)\)
\(\Leftrightarrow...\)

\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x-2}+1}{\sqrt[]{x+3}-2}=\lim\limits_{x\rightarrow1}\dfrac{\left(\sqrt[3]{x-2}+1\right)\left(\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1\right)\left(\sqrt[]{x+3}+2\right)}{\left(\sqrt[]{x+3}-2\right)\left(\sqrt[]{x+3}+2\right)\left(\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(\sqrt[]{x+3}+2\right)}{\left(x-1\right)\left(\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\sqrt[]{x+3}+2}{\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1}\)
\(=\dfrac{\sqrt[]{1+3}+2}{\sqrt[3]{\left(1-2\right)^2}-\sqrt[3]{1-2}+1}=\dfrac{4}{3}\)

1.
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow x-\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
2.
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
3.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{5}{8}\)
\(\Leftrightarrow\dfrac{3}{4}+\dfrac{1}{4}cos4x=\dfrac{5}{8}\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{2\pi}{3}+k2\pi\\4x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)

\(\lim\dfrac{3^n+2.6^n}{6^{n-1}+5.4^n}=\lim\dfrac{6^n\left[\left(\dfrac{3}{6}\right)^n+2\right]}{6^n\left[\dfrac{1}{6}+5\left(\dfrac{4}{6}\right)^n\right]}=\lim\dfrac{\left(\dfrac{3}{6}\right)^n+2}{\dfrac{1}{6}+5\left(\dfrac{4}{6}\right)^n}=\dfrac{0+2}{\dfrac{1}{6}+0}=12\)
\(\lim\left(\sqrt{n^2+9}-n\right)=\lim\dfrac{\left(\sqrt{n^2+9}-n\right)\left(\sqrt{n^2+9}+n\right)}{\sqrt{n^2+9}+n}=\lim\dfrac{9}{\sqrt{n^2+9}+n}\)
\(=\lim\dfrac{n\left(\dfrac{9}{n}\right)}{n\left(\sqrt{1+\dfrac{9}{n^2}}+1\right)}=\lim\dfrac{\dfrac{9}{n}}{\sqrt{1+\dfrac{9}{n^2}}+1}=\dfrac{0}{1+1}=0\)
\(\lim\dfrac{\sqrt{15+9n^2}-3}{5-n}=\lim\dfrac{n\sqrt{\dfrac{15}{n^2}+9}-3}{5-n}=\lim\dfrac{n\left(\sqrt{\dfrac{15}{n^2}+9}-\dfrac{3}{n}\right)}{n\left(\dfrac{5}{n}-1\right)}\)
\(=\lim\dfrac{\sqrt{\dfrac{15}{n^2}+9}-\dfrac{3}{n}}{\dfrac{5}{n}-1}=\dfrac{\sqrt{9}-0}{0-1}=-3\)

7.
\(y'=3x^2+8x-1\)
\(\Rightarrow y'\left(2\right)=3.2^2+8.2-1=27\)

Gọi E là giao điểm của AC và BD thì \(SE=\left(SAC\right)\cap\left(SBD\right)\)

Mik chưa học lớp 11 nên ko trả lời đc sorry nha !! mik mới học lớp 6 thui