
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nãy ghi nhầm =="
a)Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
Thay `m=1` vào pt ta có:
`x^2-2x-2-1=0`
`<=>x^2-2x-3=0`
`a-b+c=0`
`=>x_1=-1,x_2=3`
`=>y_1=1,y_2=9`
`=>(-1,1),(3,9)`
Vậy tọa độ gđ (d) và (P) là `(-1,1)` và `(3,9)`
b)
Hđ gđ là nghiệm pt
`x^2=2x+2m+1`
`<=>x^2-2x-2m-1=0`
PT có 2 nghiệm pb
`<=>Delta'>0`
`<=>1+2m+1>0`
`<=>2m> -2`
`<=>m> 01`
Áp dụng hệ thức vi-ét:`x_1+x_2=2,x_1.x_2=-2m-1`
Theo `(P):y=x^2=>y_1=x_1^2,y_2=x_2^2`
`=>x_1^2+x_2^2=14`
`<=>(x_1+x_2)^2-2x_1.x_2=14`
`<=>4-2(-2m-1)=14`
`<=>4+2(2m+1)=14`
`<=>2(2m+1)=10`
`<=>2m+1=5`
`<=>2m=4`
`<=>m=2(tm)`
Vậy `m=2` thì ....

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}+\sqrt{x}=2\sqrt{x}\)

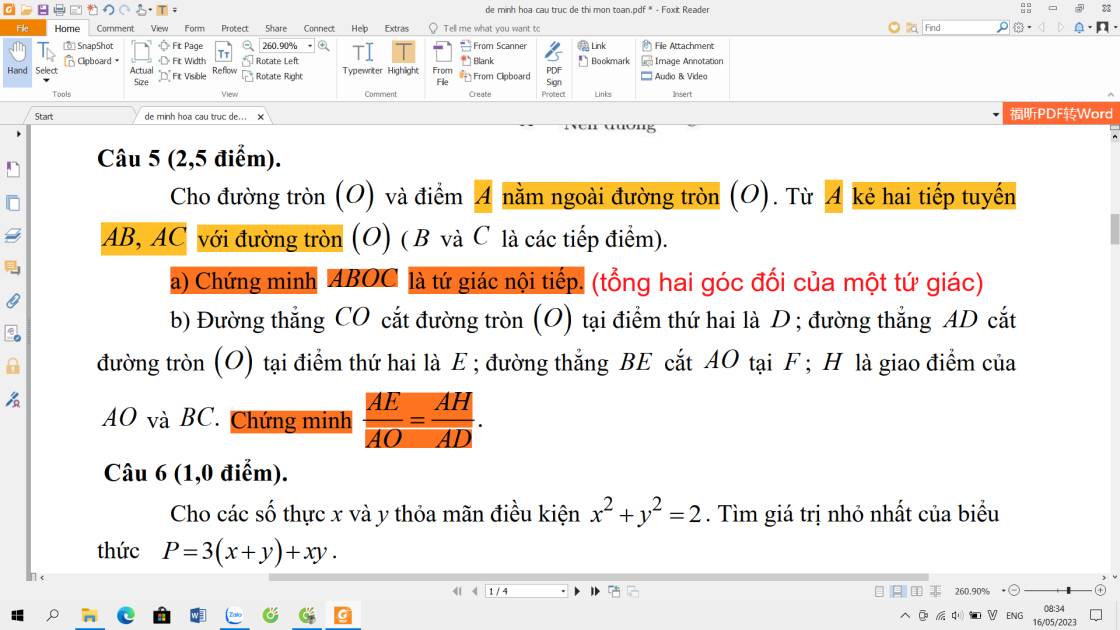
5:
a: góc ABO+góc ACO=180 độ
=>ABOC nội tiếp
b: Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB^2=AE*AD
Xet (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>AH*AO=AB^2=AE*AD
=>AE/AO=AH/AD

1:
a: Phương trình hoành độ giao điểm là:
\(-x^2=mx+2\)(1)
=>\(x^2+mx+2=0\)
\(\text{Δ}=m^2-4\cdot1\cdot2=m^2-8\)
Để (P) cắt (d) tại 1 điểm duy nhất thì phương trình (1) có 1 nghiệm duy nhất
=>Δ=0
=>\(m^2-8=0\)
=>\(m^2=8\)
=>\(m=\pm2\sqrt{2}\)
b: Thay x=-2 và y=m vào (P), ta được:
\(m=-\left(-2\right)^2=-4\)
Thay x=1 và y=n vào (d), ta được:
\(m\cdot1+2=n\)
=>-4+2=n
=>n=-2
2:
Gọi chiều dài hình chữ nhật đã cho là x(m)
(Điều kiện: x>2)
Chiều rộng hình chữ nhật đã cho là 0,5x(m)
Chiều dài hình chữ nhật khi giảm đi 2m là x-2(m)
Chiều rộng hình chữ nhật khi giảm đi 2m là 0,5x-2(m)
Diện tích ban đầu là \(0,5x\cdot x=0,5x^2\left(m^2\right)\)
Diện tích lúc sau là: \(\left(x-2\right)\cdot\left(0,5x-2\right)=0,5x^2-3x+4\left(m^2\right)\)
Diện tích lúc sau giảm đi một nửa nên ta có:
\(0,5x^2-3x+4=0,5\cdot0,5x^2=0,25x^2\)
=>\(0,25x^2-3x+4=0\)
=>\(x^2-12x+16=0\)
=>\(\left[{}\begin{matrix}x=6+2\sqrt{5}\left(nhận\right)\\x=6-2\sqrt{5}\left(loại\right)\end{matrix}\right.\)
vậy: Chiều dài ban đầu của hình chữ nhật là \(6+2\sqrt{5}\left(m\right)\)


Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{3}< >-\dfrac{1}{m}\)
=>\(m^2\ne-3\)(luôn đúng)
Ta có: \(\left\{{}\begin{matrix}mx-y=2\\3x+my=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m\left(mx-2\right)=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\3x+m^2x-2m=3m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=mx-2\\x\left(m^2+3\right)=5m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=m\cdot\dfrac{5m}{m^2+3}-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5m}{m^2+3}\\y=\dfrac{5m^2-2m^2-6}{m^2+3}=\dfrac{3m^2-6}{m^2+3}\end{matrix}\right.\)
\(\left(x+y\right)\cdot\left(m^2+3\right)+8=0\)
=>\(\dfrac{5m+3m^2-6}{m^2+3}\cdot\left(m^2+3\right)+8=0\)
=>\(3m^2+5m-6+8=0\)
=>\(3m^2+5m+2=0\)
=>(m+1)(3m+2)=0
=>\(\left[{}\begin{matrix}m=-1\\m=-\dfrac{2}{3}\end{matrix}\right.\)

\(\left(d\right):\frac{x}{a}+\frac{y}{b}=1\)\(\left(1\right)\)
Thế \(x=a,y=0\)vào phương trình \(\left(1\right)\)thỏa mãn nên \(A\left(a,0\right)\)thuộc \(\left(d\right)\).
Thế \(x=0,y=b\)vào phương trình \(\left(1\right)\)thỏa mãn nên \(B\left(0,b\right)\)thuộc \(\left(d\right)\).
Do đó ta có đpcm.

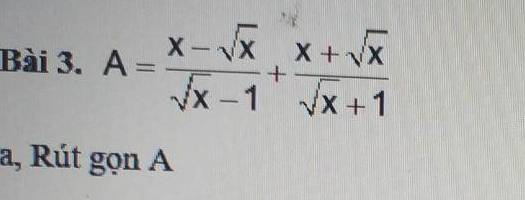
 giải giúp mình 2 câu này với ạ
giải giúp mình 2 câu này với ạ



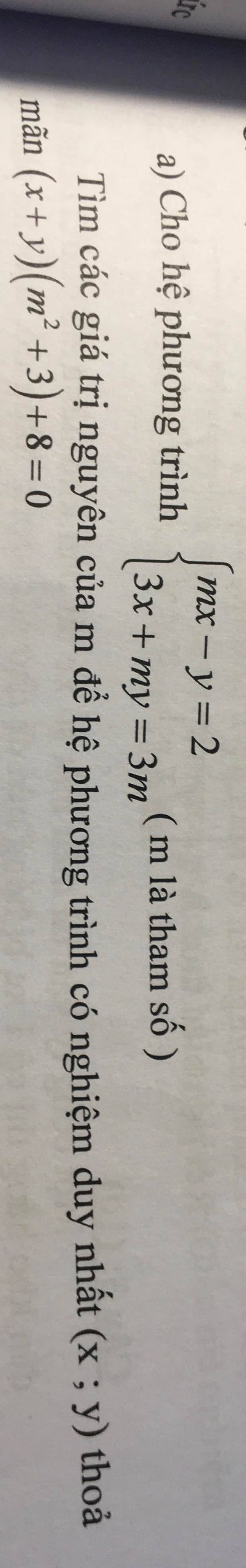
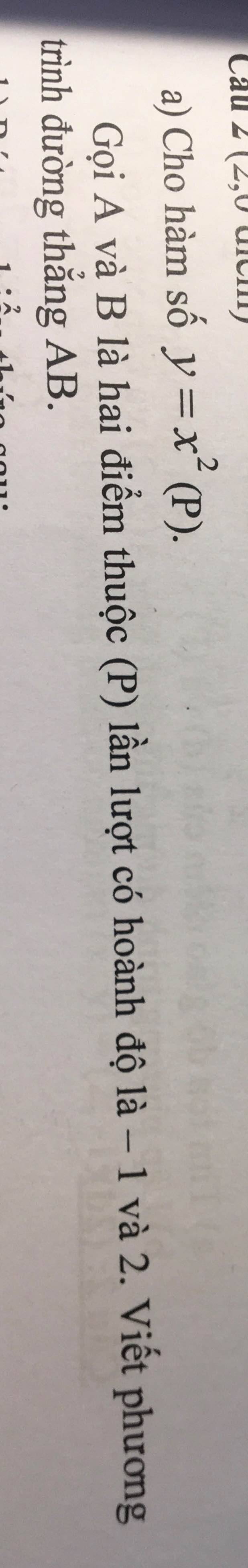
 ai giúp mình giải câu này với ạ, mình cám ơn mn nhiều
ai giúp mình giải câu này với ạ, mình cám ơn mn nhiều




\(x^2-4x+1=0\)
\(\text{Δ}=\left(-4\right)^2-4\cdot1\cdot1=16-4=12>0\)
=>Phương trình có hai nghiệm phân biệt
\(x_1+x_2=-\left(-4\right)=4;x_1\cdot x_2=1\)
\(S=x_1^2\left(x_1-x_2\right)+x_2^2\left(x_2-x_1\right)\)
\(=x_1^2\left(x_1-x_2\right)-x_2^2\left(x_1-x_2\right)\)
\(=\left(x_1-x_2\right)\left(x_1^2-x_2^2\right)\)
\(=\left(x_1+x_2\right)\left(x_1-x_2\right)^2\)
\(=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-4x_1x_2\right]\)
\(=4\cdot\left[4^2-4\cdot1\right]\)
\(=4\cdot\left(16-4\right)=4\cdot12=48\)