Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi N là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}ON\perp AB\\SO\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SON\right)\)
Từ O kẻ \(OH\perp SN\) (H thuộc SN) \(\Rightarrow OH\perp\left(SAB\right)\Rightarrow OH=d\left(O;\left(SAB\right)\right)\)
\(ON=\dfrac{1}{2}AD=\dfrac{a}{2}\) ; \(SO=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(OH=\dfrac{SO.ON}{\sqrt{SO^2+ON^2}}=\dfrac{a\sqrt{6}}{6}\)
Lại có: M là trung điểm OD \(\Rightarrow OM=\dfrac{1}{2}OD\Rightarrow BM=\dfrac{3}{2}OB\)
\(\Rightarrow d\left(M;\left(SAB\right)\right)=\dfrac{3}{2}d\left(O;\left(SAB\right)\right)=\dfrac{3}{2}.\dfrac{a\sqrt{6}}{6}=\dfrac{a\sqrt{6}}{4}\)

a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)

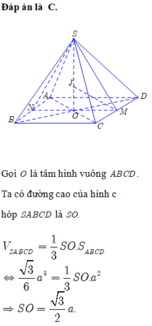
Chọn D
Khối đa diện ABCDSH được chia thành hai khối chóp S.ABCD và H.SCD

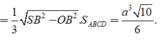
Vì H là điểm đối xứng của O qua SM nên
![]()

Vậy thể tích khối đa diện cần tính bằng
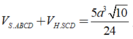
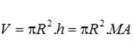
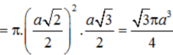
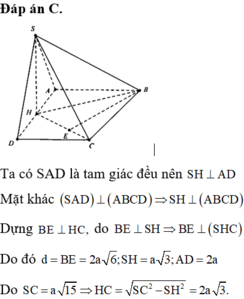
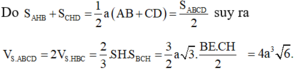
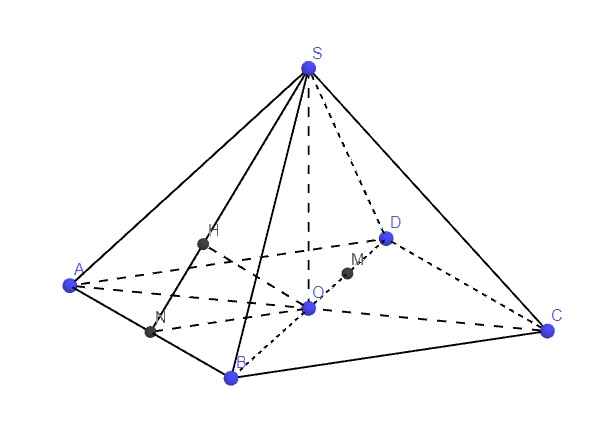
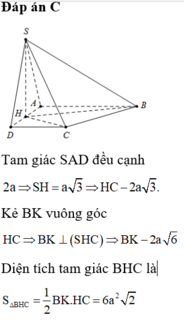
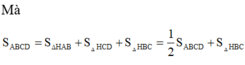
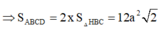
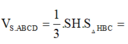
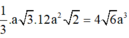

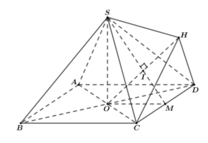
Vì `SCD` cân tại `S=>SI \bot CD`
Trong `(SCD)` có: `SI \bot CD`
`=>d(S,CD)=SI=[a\sqrt{3}]/2`
làm sao ra được kết quả đó vậy ạ?