K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2022
Gọi giá trị của chữ số sau khi xóa đi số 5 là x (với \(x>0;x\in N\))
Giá trị chữ số ban đầu: \(10x+5\)
Theo bài ra ta có pt:
\(10x+5-x=1796\)
\(\Rightarrow9x=1791\)
\(\Rightarrow x=199\)
Vậy chữ số đó là \(1995\)
17 tháng 2 2022
Phương trình hoành độ giao điểm là:
\(x^2-2mx+m^2-m=0\)
a: Để (P) cắt (d) tại hai điểm phân biệt thì \(\left(-2m\right)^2-4\left(m^2-m\right)>0\)
=>4m>0
hay m>0
b: Để (P) cắt (d) tại hai điểm nằm về hai phía của trục tung thì \(m^2-m< 0\)
=>0<m<1
29 tháng 10 2021
\(\left\{{}\begin{matrix}x=5-y\\y\left(5-y\right)=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=4\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=1\end{matrix}\right.\end{matrix}\right.\)
28 tháng 1 2022
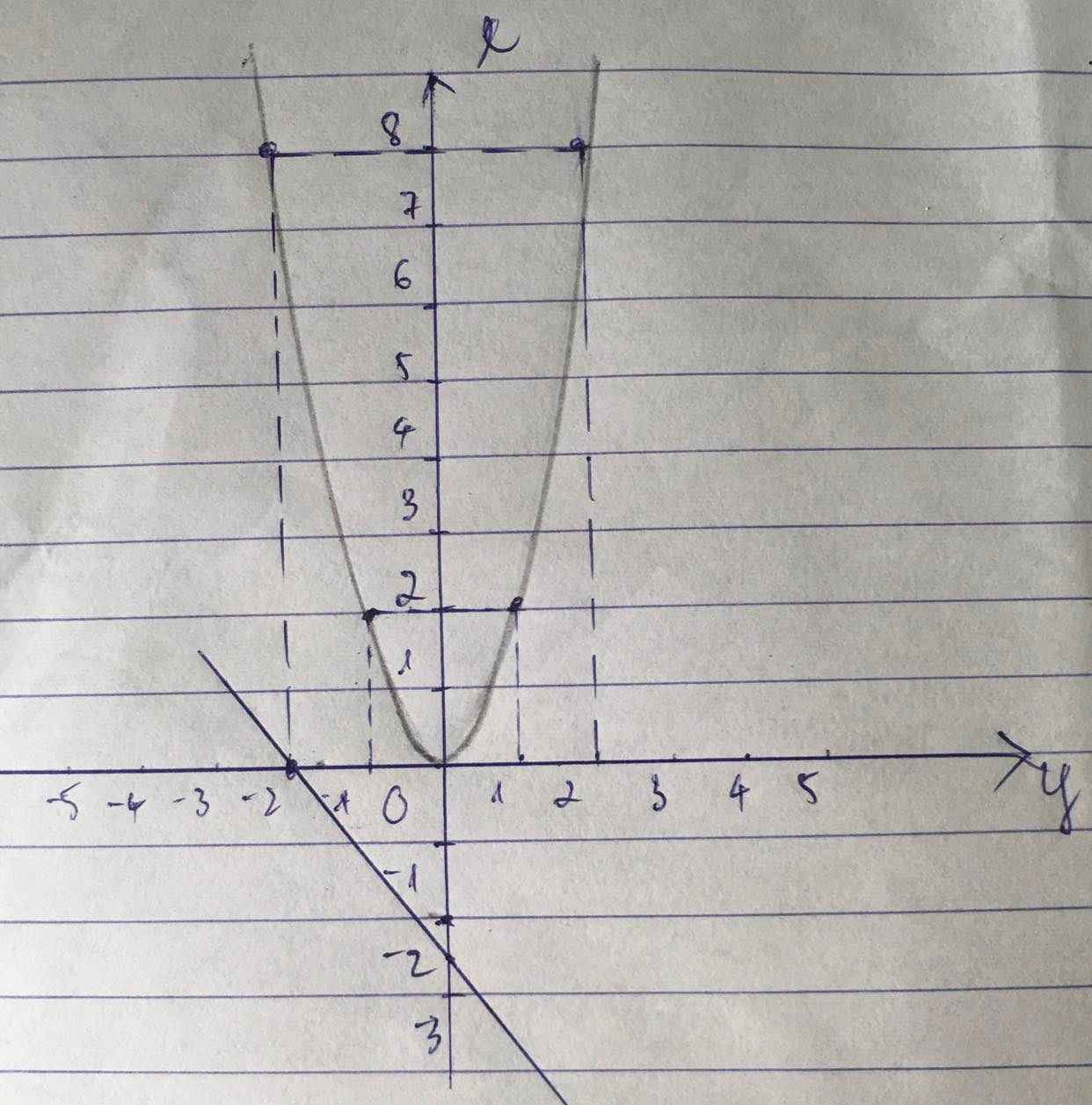
a) Thay m = -2 vào (P) ta có:
\(y=\left(-2-3\right)x+\left(-2\right).\\ \Leftrightarrow y=-5x-2.\)
i) + \(y=-5x-2.\)
\(Cho\) \(x=0.\Rightarrow y=-2.\)
\(Cho\) \(y=0.\Rightarrow x=\dfrac{-2}{5}.\)
+ \(y=2x^2.\)
| \(x\) | -2 | -1 | 0 | 1 | 2 |
| \(y=2x^2\) | 8 | 2 | 0 | 2 | 8 |
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2024
a.
- Với \(y\ge0\Rightarrow x^2+2y\ge0\) với mọi x \(\Rightarrow\) hệ vô nghiệm do \(-2< 0\)
- Với \(y< 0\Rightarrow\left|y\right|=-y\), hệ tương đương:
\(\left\{{}\begin{matrix}x^2+2y=-2\\3x^2-y=15\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2+2y=-2\\6x^2-2y=30\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+2y=-2\\7x^2=28\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x^2=4\\y=-3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\pm2\\y=-3\end{matrix}\right.\)
b.
Gọi số chính phương cần tìm là \(n^2\) với n là số tự nhiên, do \(n^2\) có 4 chữ số
\(\Rightarrow999< n^2< 10000\Rightarrow31< n< 100\)
Do khi cộng số cần tìm với 2023 ta cũng được 1 SCP
\(\Rightarrow n^2+2023=m^2\) (với m tự nhiên và \(m>n\))
\(\Rightarrow m^2-n^2=2023\)
\(\Rightarrow\left(m-n\right)\left(m+n\right)=2023\)
Ta chỉ cần xét các cặp ước của 2023 mà \(m+n>m-n\)
| m-n | 1 | 7 | 17 |
| m+n | 2023 | 289 | 119 |
| m | 1012 | 148 | 68 |
| n | 1011 | 141 | 51 |
Do \(31< n< 100\) nên chỉ có \(n=51\) thỏa mãn
Vậy số cần tìm là \(51^2=2601\)
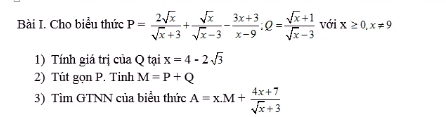
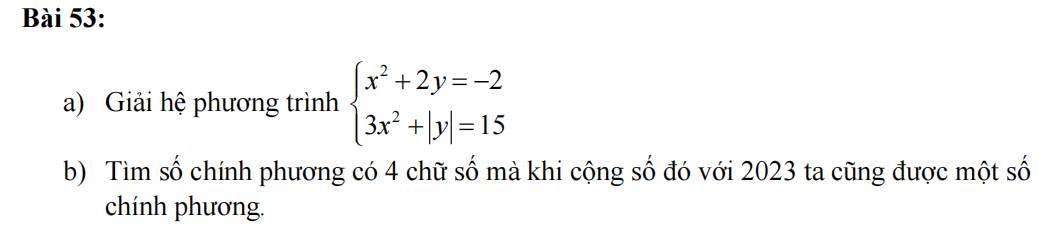
Bài nào em hỉ?