Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.png)
⇔ .png)
.png)
.png)
+ k2π ⇔ x = .png)
, (k ∈ Z)..png)
) = 0 ⇔ .png)
, (k ∈ Z)..png)
= sin(-600) nên phương trình đã cho tương đương với.png)
.png)
a) Ta có:
sin(x+1)=23⇔[x+1=arcsin23+k2πx+1=π−arcsin23+k2π⇔[x=−1+arcsin23+k2πx=−1+π−arcsin23+k2π;k∈Zsin(x+1)=23⇔[x+1=arcsin23+k2πx+1=π−arcsin23+k2π⇔[x=−1+arcsin23+k2πx=−1+π−arcsin23+k2π;k∈Z
b) Ta có:
sin22x=12⇔1−cos4x2=12⇔cos4x=0⇔4x=π2+kπ⇔x=π8+kπ4,k∈Zsin22x=12⇔1−cos4x2=12⇔cos4x=0⇔4x=π2+kπ⇔x=π8+kπ4,k∈Z
c) Ta có:
cot2x2=13⇔⎡⎢⎣cotx2=√33(1)cotx2=−√33(2)(1)⇔cotx2=cotπ3⇔x2=π3+kπ⇔x=2π3+k2π,k∈z(2)⇔cotx2=cot(−π3)⇔x2=−π3+kπ⇔x=−2π3+k2π;k∈Zcot2x2=13⇔[cotx2=33(1)cotx2=−33(2)(1)⇔cotx2=cotπ3⇔x2=π3+kπ⇔x=2π3+k2π,k∈z(2)⇔cotx2=cot(−π3)⇔x2=−π3+kπ⇔x=−2π3+k2π;k∈Z
d) Ta có:
tan(π12+12x)=−√3⇔tan(π12+12π)=tan(−π3)⇔π12+12=−π3+kπ⇔x=−5π144+kπ12,k∈Z
Vậy nghiệm của phương trình đã cho là: x=−5π144+kπ12,k∈Z
a)
\(sin\left(x+1\right)=\dfrac{2}{3}\Leftrightarrow\left[{}\begin{matrix}x+1=arcsin\dfrac{2}{3}+k2\pi\\x+1=\pi-arcsin\dfrac{2}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=arcsin\dfrac{2}{3}-1+k2\pi\\x=\pi-arcsin\dfrac{2}{3}-1+k2\pi\end{matrix}\right.\)\(\left(k\in Z\right)\).
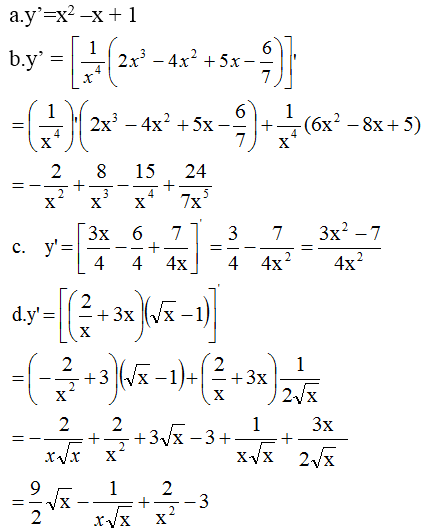
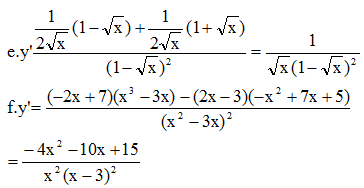
a: \(2^{x^2-1}=256\)
=>\(2^{x^2-1}=2^8\)
=>\(x^2-1=8\)
=>\(x^2=9\)
=>\(x\in\left\{3;-3\right\}\)
b: \(3^{x^2+3x}=81\)
=>\(3^{x^2+3x}=3^4\)
=>\(x^2+3x=4\)
=>\(x^2+3x-4=0\)
=>(x+4)(x-1)=0
=>\(\left[{}\begin{matrix}x+4=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=1\end{matrix}\right.\)
c: \(2^{x^2-5x}=64\)
=>\(2^{x^2-5x}=2^6\)
=>\(x^2-5x=6\)
=>\(x^2-5x-6=0\)
=>(x-6)(x+1)=0
=>\(\left[{}\begin{matrix}x-6=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-1\end{matrix}\right.\)
d: \(\left(\dfrac{1}{3}\right)^x=243\)
=>\(\left(\dfrac{1}{3}\right)^x=3^5=\left(\dfrac{1}{3}\right)^{-5}\)
=>x=-5
e: \(\left(\dfrac{1}{3}\right)^{x+5}=3^{2x+1}\)
=>\(3^{-x-5}=3^{2x+1}\)
=>-x-5=2x+1
=>-3x=6
=>x=-2