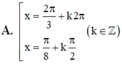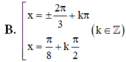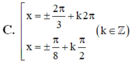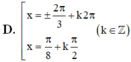K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 7 2020
\(\text{c) }sin3x-\sqrt{3}cos3x=2cos5x\\ \Leftrightarrow\frac{1}{2}sin3x-\frac{\sqrt{3}}{2}cos3x=cos5x\\ \Leftrightarrow sin\frac{\pi}{6}\cdot sin3x-cos\frac{\pi}{6}\cdot cos3x=cos5x\\ \Leftrightarrow cos\left(3x+\frac{\pi}{6}\right)=-cos5x\\ \Leftrightarrow cos\left(3x+\frac{\pi}{6}\right)=cos\left(\pi-5x\right)\\ \Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{6}=\pi-5x+m2\pi\\3x+\frac{\pi}{6}=5x-\pi+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{5\pi}{48}+\frac{m\pi}{4}\\x=\frac{7\pi}{12}-n\pi\end{matrix}\right.\)
\(d\text{) }sinx\left(sinx+2cosx\right)=2\\ \Leftrightarrow cos^2x+\left(sinx-cosx\right)^2=0\\ \Leftrightarrow cosx=sinx=0\left(VN\right)\)
\(e\text{) }\sqrt{3}\left(sin2x+cos7x\right)=sin7x-cos2x\\ \Leftrightarrow\sqrt{3}sin2x+cos2x=sin7x-\sqrt{3}cos7x\\ \Leftrightarrow sin2x\cdot\frac{\sqrt{3}}{2}+cos2x\cdot\frac{1}{2}=sin7x\cdot\frac{1}{2}-cos7x\cdot\frac{\sqrt{3}}{2}\\ \Leftrightarrow sin2x\cdot cos\frac{\pi}{3}+cos2x\cdot sin\frac{\pi}{3}=sin7x\cdot cos\frac{\pi}{3}-cos7x\cdot sin\frac{\pi}{3}\\ \Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=sin\left(7x-\frac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=7x-\frac{\pi}{3}+m2\pi\\2x-\frac{\pi}{3}=\frac{4\pi}{3}-7x+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{-m2\pi}{5}\\x=\frac{5\pi}{27}+\frac{n2\pi}{9}\end{matrix}\right.\)
15 tháng 7 2020
\(\text{a) }\sqrt{3}sin2x-cos2x+1=0\\ \Leftrightarrow\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x=-\frac{1}{2}\\ \Leftrightarrow cos\frac{\pi}{3}\cdot cos2x-sin\frac{\pi}{3}\cdot sin2x=\frac{1}{2}\\ \Leftrightarrow cos\left(2x-\frac{\pi}{3}\right)=cos\frac{\pi}{3}\\ \Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{3}+m2\pi\\2x-\frac{\pi}{3}=-\frac{\pi}{3}+n2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+m\pi\\x=n\pi\end{matrix}\right.\)
\(\text{b) }pt\Leftrightarrow sin4x=\frac{1-4cosx}{3}\\ \Leftrightarrow sin^24x+cos^24x=\left(\frac{1-cos4x}{3}\right)^2+cos^24x=1\\ \Leftrightarrow\left[{}\begin{matrix}cos4x=1\\cos4x=-\frac{4}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}cos4x=1\\cos4x=-\frac{4}{5}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{arccos\left(-\frac{4}{5}\right)}{4}+\frac{k\pi}{2}\end{matrix}\right.\)
PT
1
CM
26 tháng 2 2018
Chọn D
Ta sẽ biến đổi phương trình thành dạng tích
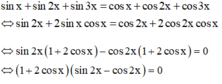
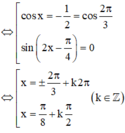
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm
TN
1
29 tháng 9 2020
Đề thiếu bạn nhé!
\(5(sinx+\frac{cos3x+sin3x}{1+2sin2x})=cos2x+3\) (*)
ĐKXĐ: 1 + 2sin2x \(\ne0\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x\ne-\frac{\pi}{12}+k\pi\\x\ne\frac{7\pi}{12}+k\pi\end{matrix}\right.\)
Biến đổi riêng biểu thức: \(\frac{cos3x+sin3x}{1+2sin2x}\)
= \(\frac{\left(4cos^3x-3cosx\right)+\left(3sinx-4sin^3x\right)}{1+2sin2x}\)
\(=\frac{4\left(cos^3x-sin^3x\right)+3\left(sinx-cosx\right)}{1+2sin2x}\)
\(=\frac{4\left(cosx-sinx\right)\left(cos^2x+sinx.cosx+sin^2x\right)-3\left(cosx-sinx\right)}{1+2sin2x}\)
= \(\frac{4\left(cosx-sinx\right)\left(1+sinx.cosx\right)-3\left(cosx-sinx\right)}{1+2sin2x}\)
= \(\frac{\left(cosx-sinx\right)\left(4+2sin2x-3\right)}{1+2sin2x}\)
= cosx - sinx
Khi đó:
(*) \(\Leftrightarrow\) 5(sinx + cosx - sinx) - cos2x - 3 = 0
\(\Leftrightarrow5cosx+1-2cos^2x-3=0\)
\(\Leftrightarrow2cos^2x-5cosx+2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=2\left(-1\le cosx\le1\right)\\cosx=\frac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\frac{\pi}{3}+k2\pi\)
Với x \(\in\left[0;2\pi\right]\Leftrightarrow\left[{}\begin{matrix}0\le\frac{\pi}{3}+k2\pi\le2\pi\\0\le-\frac{\pi}{3}+k2\pi\le2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-\frac{1}{6}\le k\le\frac{5}{6}\\\frac{1}{6}\le k\le\frac{7}{6}\end{matrix}\right.\)
k \(\in Z\Rightarrow\left[{}\begin{matrix}k=0\\k=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}\\x=\frac{5\pi}{3}\end{matrix}\right.\)
Nghiệm của pt (*) thuộc đoạn [0;\(2\pi\)] là:
S = \(\left\{\frac{\pi}{3};\frac{5\pi}{3}\right\}\)
PT
1
HL
1
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 10 2020
b.
\(\Leftrightarrow\sqrt{2}cos\left(3x+\frac{\pi}{4}\right)=-\sqrt{2}\)
\(\Leftrightarrow cos\left(3x+\frac{\pi}{4}\right)=-1\)
\(\Leftrightarrow3x+\frac{\pi}{4}=\pi+k2\pi\)
\(\Leftrightarrow x=...\)
c.
\(\Leftrightarrow\frac{\sqrt{3}}{2}sin2x+\frac{1}{2}cos2x=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(2x+\frac{\pi}{6}\right)=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\frac{\pi}{6}=-\frac{\pi}{4}+k2\pi\\2x+\frac{\pi}{6}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
CP
1
HT
1 tháng 8 2019
Em ms hok cái này nên ko chắc lắm ạ :))
a/ \(\Leftrightarrow2\sin^2x.\cos x+3\sin x-4\sin^3x-4\cos^3x=0\)
Xét \(\sin^3x=0\) ko phải là nghiệm của PT
Xét \(\sin^3x\ne0\)
\(\Leftrightarrow2.\cot x+\frac{3}{\sin^2x}-4-4.\cot^3x=0\)
\(\Leftrightarrow4\cot^3x-3\cot^2x-2\cot x+1=0\)
Sau đó chị giải nghiệm là xong, thú thật e kém về phần gpt b3 trở lên nên sợ sai lắm :))
câu b khá là dài vì phải phân tích cos^3 2x nên ngày mai e giải nốt ạ :))
TN
0