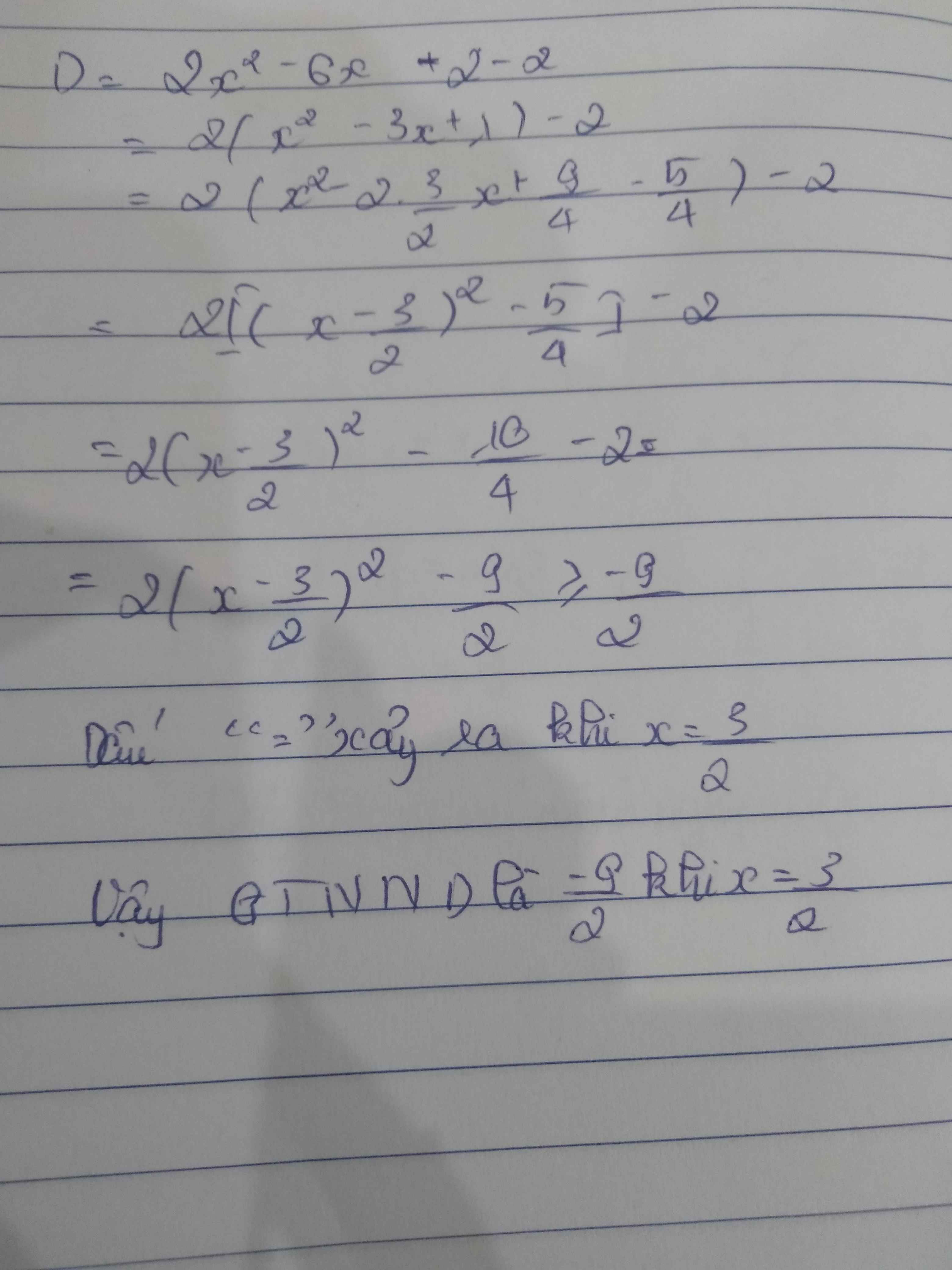Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)Ta thấy:
\(\left(2x+\frac{1}{3}\right)^2\ge0\)
\(\Rightarrow\left(2x+\frac{1}{3}\right)^2-\frac{5}{6}\ge0-\frac{5}{6}=-\frac{5}{6}\)
\(\Rightarrow A\ge-\frac{5}{6}\)
Dấu "=" <=>x=-1/6
Vậy MinA=-5/6<=>x=-1/6
b)Ta thấy:\(\hept{\begin{cases}\left|2x+3\right|\\\left|y-\frac{1}{2}\right|\end{cases}\ge}0\)
\(\Rightarrow\left|2x-3\right|+\left|y-\frac{1}{2}\right|\ge0\)
\(\Rightarrow\left|2x-3\right|+\left|y-\frac{1}{2}\right|+\frac{3}{4}\ge0+\frac{3}{4}=\frac{3}{4}\)
\(\Rightarrow B\ge\frac{3}{4}\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}\left|2x-3\right|=0\\\left|y-\frac{1}{2}\right|=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{3}{2}\\y=\frac{1}{2}\end{cases}}\)
Vậy...

a ) \(A=\left|2x-2\right|+\left|2x-2019\right|\ge\left|2-2x+2x-2019\right|=\left|2-2019\right|=2017\)
Để A đạt GTNN là 2017 <=> \(\left(2-2x\right)\left(2x-2019\right)\ge0\Rightarrow1\le x\le\frac{2019}{2}\)
b ) \(\left|2x-4\right|-\left|6-3x\right|=-1\)
\(\Leftrightarrow2\left|x-2\right|-3\left|x-2\right|=-1\)
\(\Leftrightarrow-\left|x-2\right|=-1\)
\(\Rightarrow\left|x-2\right|=1\)
\(\Rightarrow x=1;3\)
Mà x lớn nhất => x = 3

a) ta có |1-2x|>=0
=>3.|1-2x|>=0
=>A>=0-5
A>=-5
dấu "=" xảy ra kh và chỉ khi 1-2x=0
2x=1
x=1/2
Vậy GTNN của A=-5 khi x=1/2
b)ta có -|2-3x|<=0
=>B<=3/4-0
B<=3/4
dấu "=" xảy ra khi và chỉ khi 2-3x=0
3x=2
x=2/3
Vậy GTLN của B=3/4 khi x=2/3

a) ta có:|2x-1| >hoặc bằng 0 với mọi x
suy ra : | 2x-1| -10 > hoặc bằng -10 (trừ cả 2 vế cho 10 nha bạn ) với mọi x
vậy Min của a) là -10 <=> 2x-1 =10<=>x =11/2
b) vì |x +2015|+|x+2016| > hoặc bằng 0 với mọi x
=> Min b) = 0 <=> (... tìm x => x rỗng)

D= 2x2 - 6x
= 2(x2 - 3x +\(\dfrac{9}{4}\)) - \(\dfrac{9}{2}\)
= 2[x2 - 2.x.\(\dfrac{3}{2}\) + (\(\dfrac{3}{2}\))2 ] - \(\dfrac{9}{2}\)
= 2 (x - \(\dfrac{3}{2}\))2 - \(\dfrac{9}{2}\)
Ta có:
2(x - \(\dfrac{3}{2}\))2 ≥ 0 ⇒ 2 (x - \(\dfrac{3}{2}\))2 - \(\dfrac{9}{2}\) ≥ -\(\dfrac{9}{2}\)
Hay D≥ -\(\dfrac{9}{2}\)
Dấu = xảy ra ⇔ (x - \(\dfrac{3}{2}\)) = 0 ⇔ x = \(^{\dfrac{3}{2}}\)
Vậy MinD = - \(\dfrac{9}{2}\) ⇔ x = \(\dfrac{3}{2}\)

a: \(\left(2x+1\right)^4-1\ge-1\)
Dấu '=' xảy ra khi x=-1/2
b: \(\left(x^2-16\right)^2+\left|y-3\right|-2\ge-2\)
Dấu '=' xảy ra khi \(\left(x,y\right)\in\left\{\left(4;3\right);\left(-4;3\right)\right\}\)