
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



1.
\(y'=x^2-6x+5=0\Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
Dấu của y' trên trục số:

Hàm đồng biến trên các khoảng \(\left(-\infty;1\right)\) và \(\left(5;+\infty\right)\)
Hàm nghịch biến trên \(\left(1;5\right)\)
3.
TXĐ: \(D=R\backslash\left\{2\right\}\)
\(y'=\dfrac{-5}{\left(x-2\right)^2}< 0;\forall x\in D\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
4.
\(y'=4x^3+4x=4x\left(x^2+1\right)=0\Rightarrow x=0\)
Dấu của y':
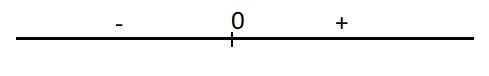
Hàm đồng biến trên \(\left(0;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;0\right)\)
6.
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-1;1\right)\)

hàm số \(y=x^0\text{ cũng chính là đường thẳng }y=1\) đây là một đường thẳng vuông góc với trục Oy tại điểm (0,1) thôi
còn hàm \(y=\frac{1}{x}\Rightarrow y'=-\frac{1}{x^2}< 0\forall x\) nên hàm số nghịch biến trên R.
Đồ thị hàm số


Gọi đường sinh là l, bán kính đáy R, chiều cao SO là h
Do thiết diện qua trục là tam giác vuông nên thiết diện là tam giác vuông cân
\(\Rightarrow SO=R\Rightarrow h=R\)
Áp dụng định lý cos: \(AB=\sqrt{OA^2+OB^2-2OA.OB.cos120^0}=R\sqrt{3}\)
Gọi H là trung điểm AB \(\Rightarrow OH\perp AB\) ; \(AH=\dfrac{AB}{2}=\dfrac{R\sqrt{3}}{2}\)
\(OH=\sqrt{OA^2-AH^2}=\dfrac{R}{2}\)
Kẻ \(OK\perp SH\Rightarrow OK\perp\left(SAB\right)\Rightarrow OK=d\left(O;\left(P\right)\right)\)
\(\dfrac{1}{SO^2}+\dfrac{1}{OH^2}=\dfrac{1}{OK^2}\Rightarrow\dfrac{1}{R^2}+\dfrac{4}{R^2}=\dfrac{5}{3a^2}\Rightarrow R=a\sqrt{3}\)
\(V=\dfrac{1}{3}\pi R^2h=\dfrac{1}{3}\pi R^3=\pi a^3\sqrt{3}\)

ta có :
\(PT\Leftrightarrow\frac{2f\left(x\right)}{f^2\left(x\right)-1}=\frac{2}{x^2}\Leftrightarrow f^2\left(x\right)-x^2f\left(x\right)-1=0\Leftrightarrow\orbr{\begin{cases}f\left(x\right)=\frac{x^2+\sqrt{x^4+4}}{2}\\f\left(x\right)=\frac{x^2-\sqrt{x^4+4}}{2}\end{cases}}\)
bằng cách lập bảng biến thiên ta xác định được phương trình trên có 4 nghiệm

Đặt \(log_2x=t\Rightarrow t\ge4\)
Phương trình trở thành: \(\sqrt{t^2-2t-3}=m\left(t-3\right)\)
\(\Leftrightarrow\sqrt{\left(t+1\right)\left(t-3\right)}=m\left(t-3\right)\)
\(\Leftrightarrow\sqrt{t+1}=m\sqrt{t-3}\)
\(\Leftrightarrow m=\sqrt{\dfrac{t+1}{t-3}}\)
Hàm \(f\left(t\right)=\sqrt{\dfrac{t+1}{t-3}}\) nghịch biến khi \(t\ge4\)
\(\lim\limits_{t\rightarrow+\infty}\sqrt{\dfrac{t+1}{t-3}}=1\) ; \(f\left(4\right)=\sqrt{5}\)
\(\Rightarrow1< f\left(t\right)\le\sqrt{5}\Rightarrow1< m\le\sqrt{5}\)
Đáp án D

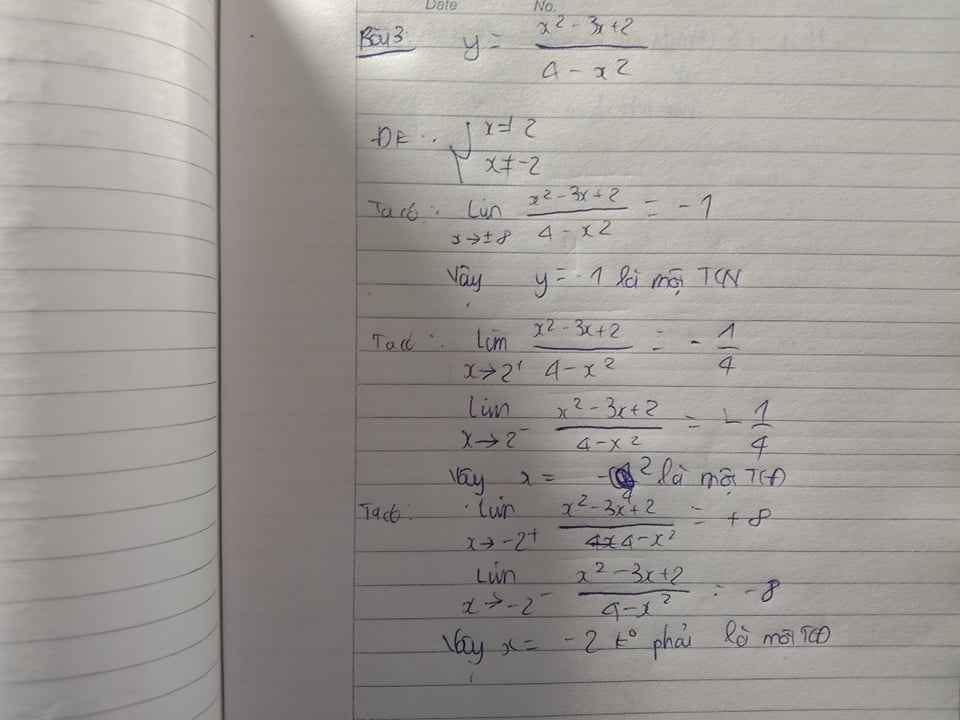
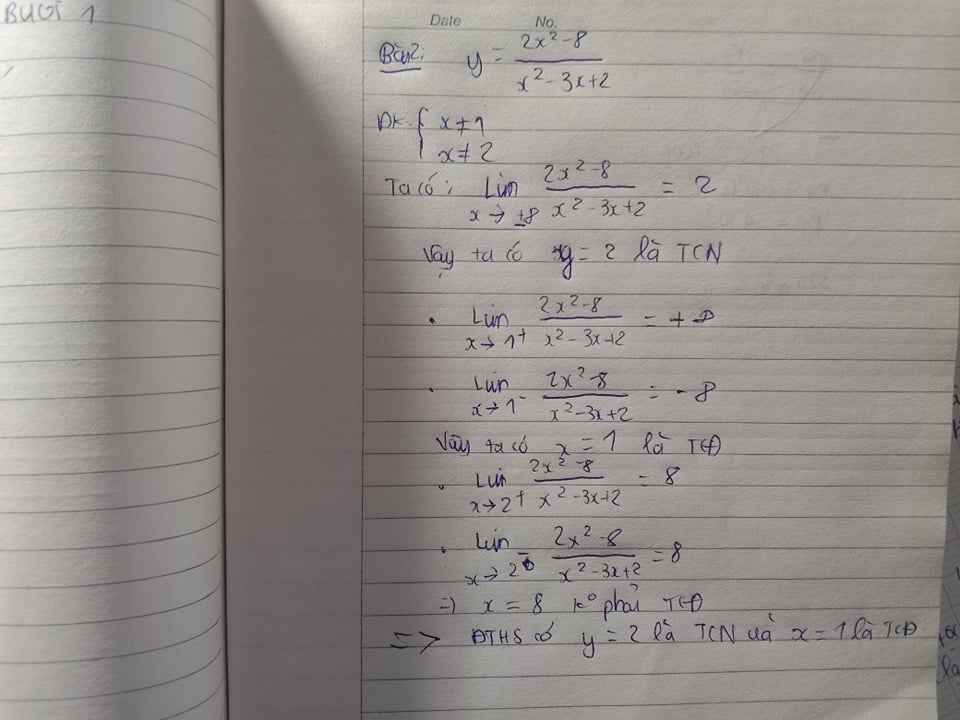


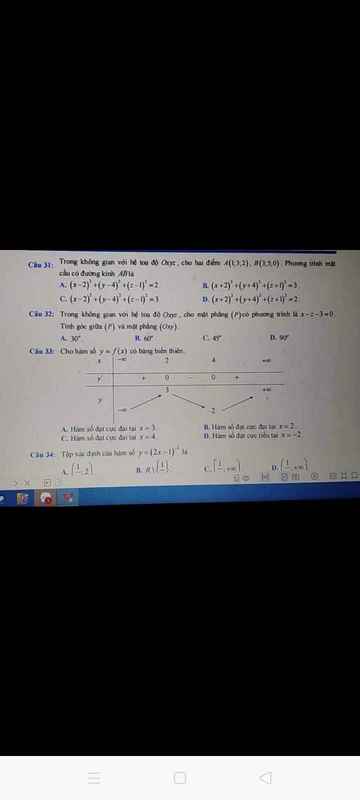

 giúp em với, khoảng sáng mai nộp ạ. Cảm ưn mn nha ^^
giúp em với, khoảng sáng mai nộp ạ. Cảm ưn mn nha ^^ d
d