Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác AHB và tam giác CHA có
góc H = 90 độ
AH là cạnh chung
góc B = góc C (kề bù)
suy ra tam giác AHB đồng dạng tam giác CHA( G.C.G)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH\cdot AH=HB\cdot HC\)
\(\Rightarrow AH^2=HB\cdot HC\)

Hình bạn tự vẽ nhé
a) Xét tam giác ABD và tam giác ACE ta có:
\(\hept{\begin{cases}\widehat{BAC}-chung\\\widehat{BDA}=\widehat{CEA}=90^o\end{cases}}\Rightarrow\Delta ABD~\Delta ACE\left(g.g\right)\)
b) H là giao điểm của BD và CE suy ra H là trực tâm của tam giác ABC
=> AH là đường cao thứ 3 của tam giác ABC => \(AH\perp BC\)
Xét \(\Delta CEB\) và \(\Delta CKH\) ta có:
\(\hept{\begin{cases}\widehat{CEB}=\widehat{CKH}=90^o\\\widehat{ECB}-chung\end{cases}}\Rightarrow\Delta CEB~\Delta CKH\left(g.g\right)\Rightarrow\frac{CE}{CK}=\frac{BC}{CH}\Rightarrow CE.CH=BC.CK\)(1)
c) Ta có: Xét \(\Delta BKH\) và \(\Delta BDC\) ta có:
\(\hept{\begin{cases}\widehat{DBC}-chung\\\widehat{HKB}=\widehat{BDC}=90^o\end{cases}}\Rightarrow\frac{BK}{BD}=\frac{BH}{BC}\Rightarrow BK.BC=BH.BD\)(2)
Cộng theo vế của (1) và (2):
\(BH.BD+CH.CE=BC\left(CK+BK\right)=BC^2\left(đpcm\right)\)

A B C H D E M K
a) Qua A kẻ đường thẳng vuông góc với tia DE tại K.
Xét tứ giác AHDK: ^AHD = ^HDK = ^AKD = 900; AH=DH => AHDK là hình vuông
=> ^HAK = 900 và AH=AK
Ta có: ^BAH + ^HAC = ^EAK + ^HAC = 900 => ^BAH = ^EAK
Xét \(\Delta\)AHB và \(\Delta\)AKE có: ^AHB = ^AKE (=900); AH=AK; ^BAH = ^EAK
=> \(\Delta\)AHB = \(\Delta\)AKE (g.c.g) => AB=AE (2 cạnh tương ứng) (đpcm).
b) Xét \(\Delta\)ABE vuông tại A có trung tuyến AM => AM=BE/2. Tương tự: DM=BE/2
=> AM=DM => \(\Delta\)MAH = \(\Delta\)MDH (c.c.c) => ^AHM = ^DHM = ^AHD/2 = 450.
ĐS...

Xét ΔEHA vuông tại E và ΔABC vuông tại A có
góc EAH=góc ACB
=>ΔEHA đồng dạng với ΔABC
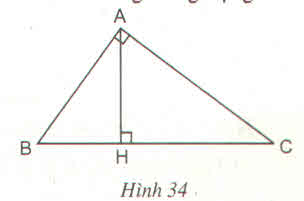

A H B C
Xét \(\Delta\)ABH và \(\Delta\)CAH có:\(\widehat{AHB}=\widehat{AHC}=90^0;\widehat{BAH}=\widehat{HCA}\)
\(\Rightarrow\Delta ABH~\Delta CAH\left(g.g\right)\Rightarrow\frac{AH}{CH}=\frac{BH}{AH}\Rightarrow AH^2=BH\cdot CH\)
\(\Rightarrowđpcm\)