Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Mô tả cách làm:
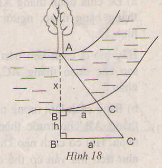
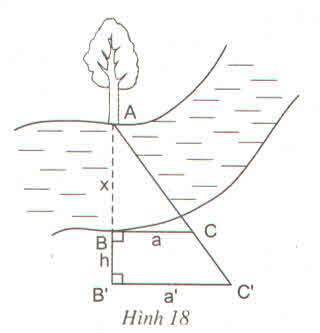
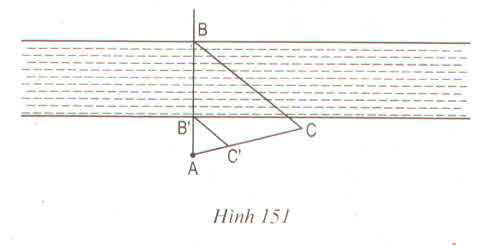
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 
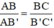(hệ quả định lý Talet)
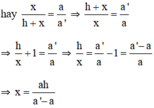
Ta có hình như sau :
giải :
Ta có:
=
mà AB' = x + h nên
=
<=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng
Ta có hình như sau :
Giải
Ta có:
=
mà AB' = x + h nên
=
<=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=
Vậy khoảng cách AB bằng
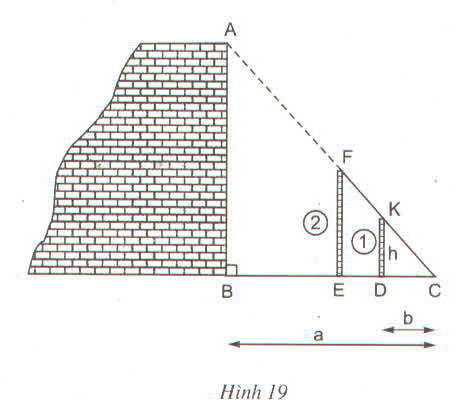
- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A,F,K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất( 3 điểm F,K,C thẳng hàng).
b) ∆BC có AB // EF nên EFABEFAB = ECBCECBC => AB = EF.BCECEF.BCEC = h.abh.ab
Vậy chiều cao của bức tường là: AB = h.abh.ab.
a) Cách đo:
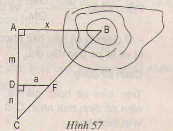
- Chọn thêm hai điểm D và C sao cho A, D, C thẳng hàng và AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thẳng hàng và DF ⊥ AC.
Giải:
a) Cách đo: Chọn thêm hai điểm C và D sao cho A,D,C thẳng hàng AC ⊥ AB.
- Chọn điểm B sao cho C, F, B thằng hàng và DF ⊥ AC.
b) ∆CDF ∽ ∆CAB (DF // AB)
=> DFAB=CDCADFAB=CDCA = > AB = DF.CACD=a(m+n)mDF.CACD=a(m+n)m
vẫy x= DF.CACD=a(m+n)mDF.CACD=a(m+n)m
a) Lều là lăng trụ đứng tam giác.
Diện tích đáy (tam giác):
S=12.3,2.1,2=1,92(m2)S=12.3,2.1,2=1,92(m2)
Thể tích khoảng không bên trong lều là:
V = Sh = 1,92. 5 = 9,6 (m3)
b) Số vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là 5m và 3,2m.
Diện tích xung quanh lăng trụ là:
Sxq = 2ph = (2 + 2+ 3,2) .5 = 36 (m2)
Diện tích toàn phần:
Stp = Sxq + 2Sđ = 36 + 2.1,92 = 39,84 (m2)
Diện tích mặt bên kích thước 5m và 3,2m là:
S = 5.3,2 = 16 (m2)
Vậy số vải bạt cần có để dựng lều là:
39,84 – 16 = 23,84 (m2)
Chú ý:Có thể tính bằng cách khác là tổng diện tích hai mặt bên và hai đáy.
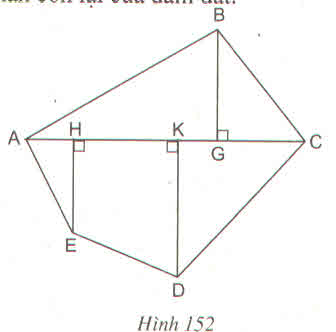
Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình vuông HKDE.
Thực hiện phép đo chính xác đến mm ta được:
BG= 19mm, AC = 48mm, AH = 8mm, HK = 18mm
KC = 22mm, EH = 16mm, KD = 23mm
Nên SABC = \(\dfrac{1}{2}\).BG. AC = \(\dfrac{1}{2}\) 19.48 = 456 (mm2)
SAHE = 1212 AH. HE =\(\dfrac{1}{2}\)8.16 = 64 (mm2)
SDKC = \(\dfrac{1}{2}\) KC.KD = \(\dfrac{1}{2}\)22.23 = 253(mm2)
SHKDE = (HE+KD).HK2(HE+KD).HK2 = (16+23).182(16+23).182= 351 (mm2)
Do đó
SABCDE = SABC + SAHE + SDKC + SHKDE = 456 + 64 + 253+ 351
Vậy SABCDE = 1124(mm2)
Đa giác ABCDE được chia thành tam giác ABC, hai tam giác vuông AHE, DKC và hình vuông HKDE.
Thực hiện phép đo chính xác đến mm ta được:
BG= 19mm, AC = 48mm, AH = 8mm, HK = 18mm
KC = 22mm, EH = 16mm, KD = 23mm
Nên SABC = 1/2.BG. AC = 1/2. 19.48 = 456 (mm2)
SAHE = 1/2 AH. HE = 1/2. 8.16 = 64 (mm2)
SDKC = 1/2 KC.KD = 1/2. 22.23 = 253(mm2)
SHKDE = (HE + KD).HK / 2 = (16 + 23).18 / 2= 351 (mm2)
Do đó
SABCDE = SABC + SAHE + SDKC + SHKDE = 456 + 64 + 253+ 351
Vậy SABCDE = 1124(mm2)
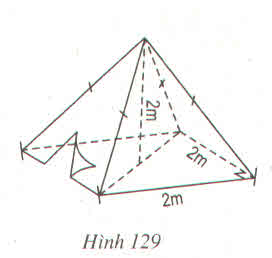
Thể tích cần tính bằng thể tích của hình chóp có chiều cao 2cm
Đáy là hình vuông cạnh dài 2m. Diện tích đáy Sđ = 22 = 4(m2)
Thể tích hình chóp : V = 1313.S.h = 1313.4.2 = 8383
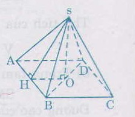
b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.
Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao SH của mỗi mặt
SH2 = SO2 + OH2 = SO2+ (BC2)2(BC2)2 = 22 + 12 = 5
SH = √5 ≈ 2,24m
Nên Sxq = p.d = 1212 2.4.2.24 = 8,96 (m2)
Thể tích cần tính bằng thể tích của hình chóp có chiều cao 2cm
Đáy là hình vuông cạnh dài 2m. Diện tích đáy Sđ = 22 = 4(m2)
Thể tích hình chóp : \(V=\dfrac{1}{3}.S.h=\dfrac{1}{3}.4.2=\dfrac{8}{3}\)
b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.
Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao SH của mỗi mặt
\(SH^2=SO^2+OH^2=SO^2+\left(\dfrac{BC}{2}\right)^2=2^2+1^2=5\)
\(SH=\sqrt{5}\approx2,24m\)
Nên Sxq = p.d = \(\dfrac{1}{2}\) 2.4.2.24 = 8,96 (m2)
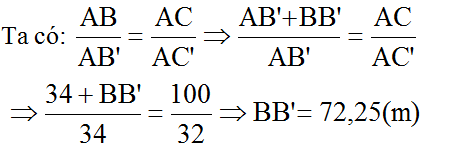
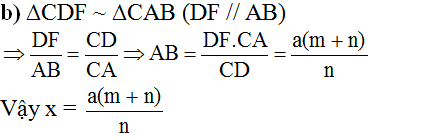
Ta có:
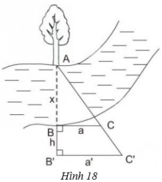
ABAB′ABAB′ = BCBC′BCBC′ mà AB' = x + h nên
xx+hxx+h = aa′aa′ <=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x= aha′−aaha′−a
Vậy khoảng cách AB bằng aha′−a