Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Q=a√a2−b2−(1+a√a2−b2):ba−√a2−b2=a√a2−b2−a2−(a2−b2)b√a2−b2=a√a2−b2−a2−a2+b2b√a2−b2=a−b√a2−

LG a
(1−a√a1−√a+√a).(1−√a1−a)2=1(1−aa1−a+a).(1−a1−a)2=1 với a≥0a≥0 và a≠1a≠1
Phương pháp giải:
+ Biến đối vế trái thành vế phải ta sẽ có điều cần chứng minh.
+ √A2=|A|A2=|A|.
+ |A|=A|A|=A nếu A≥0A≥0,
|A|=−A|A|=−A nếu A<0A<0.
+ Sử dụng các hằng đẳng thức:
a2+2ab+b2=(a+b)2a2+2ab+b2=(a+b)2
a2−b2=(a+b).(a−b)a2−b2=(a+b).(a−b).
a3−b3=(a−b)(a2+ab+b2)a3−b3=(a−b)(a2+ab+b2).
Lời giải chi tiết:
Biến đổi vế trái để được vế phải.
Ta có:
VT=(1−a√a1−√a+√a).(1−√a1−a)2VT=(1−aa1−a+a).(1−a1−a)2
=(1−(√a)31−√a+√a).(1−√a(1−√a)(1+√a))2=(1−(a)31−a+a).(1−a(1−a)(1+a))2
=((1−√a)(1+√a+(√a)2)1−√a+√a).(11+√a)2=((1−a)(1+a+(a)2)1−a+a).(11+a)2
=[(1+√a+(√a)2)+√a].1(1+√a)2=[(1+a+(a)2)+a].1(1+a)2
=[(1+2√a+(√a)2)].1(1+√a)2=[(1+2a+(a)2)].1(1+a)2
=(1+√a)2.1(1+√a)2=1=VP=(1+a)2.1(1+a)2=1=VP.
LG b
a+bb2√a2b4a2+2ab+b2=|a|a+bb2a2b4a2+2ab+b2=|a| với a+b>0a+b>0 và b≠0b≠0
Phương pháp giải:
+ Biến đối vế trái thành vế phải ta sẽ có điều cần chứng minh.
+ √A2=|A|A2=|A|.
+ |A|=A|A|=A nếu A≥0A≥0,
|A|=−A|A|=−A nếu A<0A<0.
+ Sử dụng các hằng đẳng thức:
a2+2ab+b2=(a+b)2a2+2ab+b2=(a+b)2
a2−b2=(a+b).(a−b)a2−b2=(a+b).(a−b).
a3−b3=(a−b)(a2+ab+b2)a3−b3=(a−b)(a2+ab+b2).
Lời giải chi tiết:
Ta có:
VT=a+bb2√a2b4a2+2ab+b2VT=a+bb2a2b4a2+2ab+b2
=a+bb2√(ab2)2(a+b)2=a+bb2(ab2)2(a+b)2
=a+bb2√(ab2)2√(a+b)2=a+bb2(ab2)2(a+b)2
=a+bb2|ab2||a+b|=a+bb2|ab2||a+b|
=a+bb2.|a|b2a+b=|a|=VP=a+bb2.|a|b2a+b=|a|=VP
Vì a+b>0⇒|a+b|=a+ba+b>0⇒|a+b|=a+b.

a: \(Q=\dfrac{a}{\sqrt{a^2-b^2}}-\dfrac{\sqrt{a^2-b^2}+a}{\sqrt{a^2-b^2}}\cdot\dfrac{a-\sqrt{a^2-b^2}}{b}\)
\(=\dfrac{ab}{b\left(\sqrt{a^2-b^2}\right)}-\dfrac{a^2-\left(a^2-b^2\right)}{b\sqrt{a^2-b^2}}\)
\(=\dfrac{ab-a^2+a^2-b^2}{b\sqrt{a^2-b^2}}=\dfrac{ab-b^2}{b\sqrt{a^2-b^2}}=\dfrac{a-b}{\sqrt{a^2-b^2}}\)
b: Khi a=3b thì \(Q=\dfrac{3b-b}{\sqrt{9b^2-b^2}}=\dfrac{2b}{\sqrt{8b^2}}=\dfrac{2b}{2\sqrt{2}\cdot b}=\dfrac{1}{\sqrt{2}}\)

Với \(x>0;x\ne1\)
\(M=\left(\frac{1}{a-\sqrt{a}}+\frac{1}{\sqrt{a}-1}\right):\frac{\sqrt{a}+1}{a-2\sqrt{a}+1}\)
\(=\left(\frac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}+\frac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\frac{\sqrt{a}+1}{\left(\sqrt{a}-1\right)^2}\)
\(=\frac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\frac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\frac{\sqrt{a}-1}{\sqrt{a}}\)
\(=1-\frac{1}{\sqrt{a}}< 1\)hay M < 1

a) Ta có : Vì \(x\ge0\)và \(y\ge0\)nên \(x+y\ge0\)\(\Leftrightarrow\left|x+y\right|=x+y\)
\(\frac{2}{x^2-y^2}\sqrt{\frac{3\left(x+y\right)^2}{2}}\)
\(=\frac{2}{x^2-y^2}\sqrt{\frac{3}{2}.\left(x+y\right)^2}\)
\(=\frac{2}{x^2-y^2}.\sqrt{\frac{3}{2}}.\left|x+y\right|\)
\(=\frac{2}{\left(x-y\right)\left(x+y\right)}.\sqrt{\frac{3}{2}}.\left(x+y\right)\)
\(=\frac{2}{x-y}.\sqrt{\frac{3}{2}}\)
\(=\frac{1}{x-y}.2.\sqrt{\frac{3}{2}}\)
\(=\frac{1}{x-y}.\sqrt{\frac{2^2.3}{2}}\)
\(=\frac{1}{x-y}.\sqrt{6}=\frac{\sqrt{6}}{x-y}\)
a, \(\frac{2}{x^2-y^2}\sqrt{\frac{3\left(x+y\right)^2}{2}}=\frac{2}{x^2-y^2}\frac{\sqrt{3}\left|x+y\right|}{\sqrt{2}}=\frac{2\sqrt{3}\left(x+y\right)}{\left(x-y\right)\left(x+y\right)\sqrt{2}}\)
do \(x\ge0;y\ge0\)
\(=\frac{2\sqrt{3}}{\sqrt{2}\left(x-y\right)}=\frac{2\sqrt{6}}{2\left(x-y\right)}=\frac{\sqrt{6}}{x-y}\)

\(a,Q=\frac{a}{\sqrt{a^2-b^2}}-\left(1+\frac{a}{\sqrt{a^2-b^2}}\right):\left(\frac{b}{a-\sqrt{a^2-b^2}}\right)\)
\(=\frac{a}{\sqrt{a^2-b^2}}-\left(\frac{\sqrt{a^2-b^2}+a}{\sqrt{a^2-b^2}}\right):\frac{b}{a-\sqrt{a^2+b^2}}\)
\(=\frac{a}{\sqrt{a^2-b^2}}-\frac{a+\sqrt{a^2-b^2}}{\sqrt{a^2-b^2}}.\frac{a-\sqrt{a^2-b^2}}{b}\)\(=\frac{a}{\sqrt{a^2-b^2}}-\frac{a^2-\left(a^2-b^2\right)}{b\sqrt{a^2-b^2}}\)
\(=\frac{ab-a^2+a^2-b^2}{b\sqrt{a^2-b^2}}\)
\(=\frac{b\left(a-b\right)}{b\sqrt{a^2-b^2}}=\frac{\left(a-b\right)}{\sqrt{\left(a-b\right)\left(a+b\right)}}=\frac{\sqrt{a-b}}{\sqrt{a+b}}\)
\(b.\frac{\sqrt{3b-b}}{\sqrt{3b+b}}=\frac{\sqrt{2b}}{\sqrt{4b}}=\frac{\sqrt{2}.\sqrt{b}}{2\sqrt{b}}=\frac{\sqrt{2}}{2}\)

a: \(=\dfrac{\sqrt{a}-1}{\sqrt{a}\left(a-\sqrt{a}+1\right)}\cdot\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{1}\)
\(=a-1\)
b: \(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\left(\dfrac{\sqrt{b}}{\sqrt{a}\left(\sqrt{a}-\sqrt{b}\right)}+\dfrac{\sqrt{b}}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}\right)\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{\sqrt{a}-\sqrt{b}}{2\sqrt{ab}}\cdot\dfrac{\sqrt{ab}+b+\sqrt{ab}-b}{\sqrt{a}\left(a-b\right)}\)
\(=\dfrac{\sqrt{a}+\sqrt{b}-1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}+\dfrac{1}{\sqrt{a}\left(\sqrt{a}+\sqrt{b}\right)}=\dfrac{1}{\sqrt{a}}\)
c: \(=\dfrac{a\sqrt{b}+b}{a-b}\cdot\sqrt{\dfrac{ab+b^2-2b\sqrt{ab}}{a^2+2a\sqrt{b}+b}}\cdot\left(\sqrt{a}+\sqrt{b}\right)\)
\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\sqrt{\dfrac{b\left(\sqrt{a}-\sqrt{b}\right)^2}{\left(a+\sqrt{b}\right)^2}}\)
\(=\dfrac{\sqrt{b}\left(a+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{\sqrt{b}\left(\sqrt{a}-\sqrt{b}\right)}{a+\sqrt{b}}=b\)

:") Làm bừa nhezzz
a) \(Q=\frac{a}{\sqrt{a^2-b^2}}-\left(1+\frac{a}{\sqrt{a^2-b^2}}\right):\frac{b}{a-\sqrt{a^2}-b^2}\)
\(=\frac{a}{\sqrt{a^2-b^2}}-\frac{a+\sqrt{a^2-b^2}}{\sqrt{a^2-b^2}}.\frac{a-\sqrt{a^2-b^2}}{b}\)
\(=\frac{a}{\sqrt{a^2-b^2}}-\frac{a^2-\left(\sqrt{a^2-b^2}\right)^2}{b.\left(\sqrt{a^2-b^2}\right)}\)
\(=\frac{a}{\sqrt{a^2-b^2}}-\left(\frac{a^2-\left(a^2-b^2\right)}{b.\left(\sqrt{a^2-b^2}\right)}\right)\)
\(=\frac{a}{\sqrt{a^2-b^2}}-\frac{b^2}{b\sqrt{a^2-b^2}}\)
\(=\frac{a}{\sqrt{a^2-b^2}}-\frac{b}{\sqrt{a^2-b^2}}\)
\(=\frac{a-b}{\sqrt{a^2-b^2}}=\frac{a-b}{\sqrt{\left(a-b\right)\left(a+b\right)}}=\frac{\sqrt{a-b}}{\sqrt{a+b}}\)
b) Thay a = 3b vào , ta được :
\(Q=\frac{\sqrt{3b-b}}{\sqrt{3b+b}}=\frac{\sqrt{2b}}{\sqrt{4b}}=\sqrt{\frac{2b}{4b}}=\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2}\)
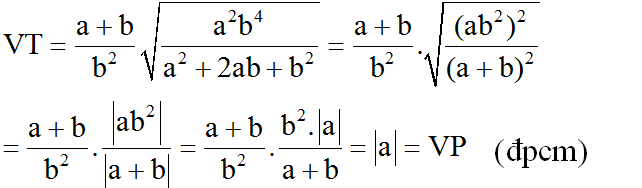

bạn tham khảo nha : https://loigiaihay.com/bai-76-trang-41-sgk-toan-9-tap-1-c44a26988.html