Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phân tích:
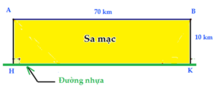
● Ta có thể mô tả bài toán trên bằng hình vẽ sau:
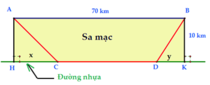
● Như đã phân tích ở trên, nếu đi trực tiếp từ A đến B trên sa mạc với vận tốc và khoảng cách hiện có thì nhà địa chất học không thể đến đúng thời gian quy định
● Vì vậy cần thiết phải chia quãng đường đi được thành 3 giai đoạn:
Giai đoạn 1: đi từ A đến C (từ sa mạc đến đường nhựa song song)
Giai đoạn 2: đi từ C đến D (một quãng đường nào đó trên đường nhựa)
Giai đoạn 3: đi từ D đến B (từ điểm kết thúc D trên đường nhựa đi tiếp đến B băng qua sa mạc).
Goi H, K, C, D là các điểm như hình vẽ.

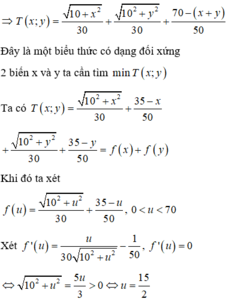
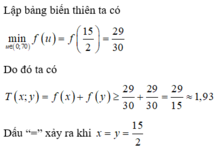

Câu trả lời
Điểm tối đa: Câu trả lời là từ 103 tới 105. Câu trả lời được chấp nhận được tính bởi công thức bằng 1/6 của chu vi hình tròn bao quanh căn phòng. Câu trả lời bằng 100 cũng được chấp nhận, nếu thí sinh tính pi = 3. Nếu trả lời là 100 và không đưa ra giải thích như trên, câu trả lời sẽ không được tính điểm (bởi thí sinh có thể đã đoán câu trả lời bằng với chiều dài của cánh cửa, tức là bán kính của hình tròn).
Không tính điểm: Tất cả các câu trả lời khác. Không tính câu trả lời 209 (tương đương với tổng kích cỡ của cả 2 cửa, thay vì mỗi cửa như yêu cầu đề bài).
Giải thích
Để đạt điểm tối đa, thí sinh phải trả lời rằng kích cỡ tối đa của cánh cửa là 1/6 của chu vi đường tròn, tính ra chính xác bằng đơn vị cen-ti-mét.

Theo như biểu đồ ở phía trên, không khí sẽ di chuyển từ bên ngoài qua cửa vào tới thẳng cửa ra nếu như phần tường nằm giữa cửa ra và cửa vào ngắn hơn phần chu vi 2 cánh cửa liên tiếp chặn lại. Do mỗi phần tường có kích cỡ bằng đúng 1/3 chu vi căn phòng, và có 2 cánh cửa tương đương với 2/3 chu vi, do đó tổng kích cỡ cửa ra và cửa vào phải nhỏ hơn 1 – 2/3 = 1/3 chu vi. Do cửa ra và cửa vào có kích cỡ bằng nhau, mỗi cánh cửa sẽ phải nhỏ hơn (1/3)/2 = 1/6 chu vi của căn phòng.
Câu trả lời
Điểm tối đa: Câu trả lời là từ 103 tới 105. Câu trả lời được chấp nhận được tính bởi công thức bằng 1/6 của chu vi hình tròn bao quanh căn phòng. Câu trả lời bằng 100 cũng được chấp nhận, nếu thí sinh tính pi = 3. Nếu trả lời là 100 và không đưa ra giải thích như trên, câu trả lời sẽ không được tính điểm (bởi thí sinh có thể đã đoán câu trả lời bằng với chiều dài của cánh cửa, tức là bán kính của hình tròn).
Không tính điểm: Tất cả các câu trả lời khác. Không tính câu trả lời 209 (tương đương với tổng kích cỡ của cả 2 cửa, thay vì mỗi cửa như yêu cầu đề bài).
Giải thích
Để đạt điểm tối đa, thí sinh phải trả lời rằng kích cỡ tối đa của cánh cửa là 1/6 của chu vi đường tròn, tính ra chính xác bằng đơn vị centi-mét.

Theo như biểu đồ ở phía trên, không khí sẽ di chuyển từ bên ngoài qua cửa vào tới thẳng cửa ra nếu như phần tường nằm giữa cửa ra và cửa vào ngắn hơn phần chu vi 2 cánh cửa liên tiếp chặn lại. Do mỗi phần tường có kích cỡ bằng đúng 1/3 chu vi căn phòng, và có 2 cánh cửa tương đương với 2/3 chu vi, do đó tổng kích cỡ cửa ra và cửa vào phải nhỏ hơn 1 – 2/3 = 1/3 chu vi. Do cửa ra và cửa vào có kích cỡ bằng nhau, mỗi cánh cửa sẽ phải nhỏ hơn (1/3)/2 = 1/6 chu vi của căn phòng.
Câu hỏi trên là một trong các câu hỏi khó nhất trong kì thi PISA, nằm ở phần trên của hạng khó nhất (Hạng 6). Câu hỏi này đòi hỏi thí sinh phải có tư duy tốt về hình học (không gian và hình dạng). Cũng bởi độ khó của câu hỏi này, thí sinh chỉ có thể đạt điểm tối đa, hoặc không đạt điểm nào. Dù chỉ đòi hỏi tư duy toán học căn bản, câu hỏi này đòi hỏi thí sinh phải phân tích một cách cẩn thận dựa trên tư duy hình học.

Đáp án C
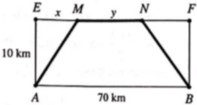
B M = x k m , 0 < x < 25 ta có
A M = A B 2 + B M 2 = x 2 + 100 = x 2 + 100 k m , M C = B C − B M = 25 − x k m
Thời gian bạn A đi xe buýt từ nhà đến điểm hẹnM là t A = x 2 + 100 30 h
Thời gian bạn A, B đi xe máy từ điểm hẹn M đến nhà bạn C là t A B = 25 − x 50 h
Suy ra thời gian bạn A đi từ nhà đến nhà bạn C là t x = t A + t A B = x 2 + 100 30 + 25 − x 50 h
Để bạn A đến nhà bạn C nhanh nhất thì hàm số t(x) đạt giá trị nhỏ nhất, với 0 < x < 25
Ta có t ' x = x 30 x 2 + 100 + 1 50 ; t ' x = 0 ⇔ x = 15 2
Lập bảng biến thiên, ta thấy hàm số t(x) đạt giá trị nhỏ nhất bằng t 15 2 = 23 30 h khi x = 15 2 k m = B M ⇒ M C = 25 − x = 35 2 k m .
Khi đó 5 B M + 3 M C = 5. 15 2 + 3. 35 2 = 90

2.
Gọi quãng đường cần tìm là s.---> vận tốc Xuân= s/12,
--> vận tốc Hạ=s/10
thời gian Xuân gặp Hạ: 50/(s/12)= (s-50)/(s/10)
50x12/s= (s-50)x10/s
50x12=10s-500
---> s = (500+50x12)/10= 110
quãng đường giữa nhà hai bạn là 110m
4.
Khi ngược dòng 1 giờ ta đi được số phần quãng sông là:
1 : 8 = 1/8 (quãng sông)
Khi xuôi dòng 1 giờ ta đi được số phần quãng sông là:
1 : 4 = 1/4 (quãng sông)
Bèo trôi theo ta về 1 giờ trôi được số phần quãng sông là:
(1/4 - 1/8) : 2 = 1/16 (quãng sông)
Bèo trôi theo ta về cập bến sau số giờ là:
1 : 1/16 = 16 (giờ)
Đ/s: 16 giờ

Chọn C.
Phương pháp:
Gắn hệ trục tọa độ, xác định tọa độ điểm M trên parabol y = x 2 để độ dài đoạn AM nhỏ nhất.
Cách giải:
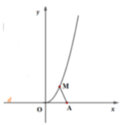
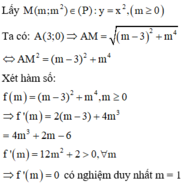
Ta có bảng biến thiên sau:
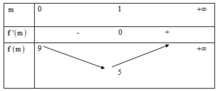
![]()

Hướng dẫn giải
Anh có thể làm việc không nhiều hơn 22 giờ một tuần : x + y ≤ 22
Anh muốn kiếm tối thiểu 1.900.000 đồng một tuần : 100.000x + 80.000y ≥ 1.900.000.
Chọn A.





Đáp án C.
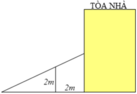
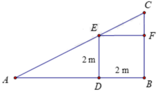
Màn biểu diễn của Dynano được biểu diễn theo mô hình bên
Cách 1: Áp dụng kiến thức “Giá trị lớn nhất – Giá trị nhỏ nhất của hàm số”
Ta có A B = c , A C = a , A D = b , A M = x . Khi đó C M = A C 2 + A M 2 = x 2 + a 2
Và
M D = B M 2 + B D 2 = ( c − x ) 2 + b 2 = x 2 − 2 c x + b 2 + c 2
Như vậy quãng đường di chuyển của Dynano là
T = C M + M D = x 2 + a 2 + x 2 − 2 c x + b 2 + c 2 ( 0 < x < c ) .
Xét hàm số x 2 + a 2 + x 2 − 2 c x + b 2 + c 2 trên ( 0 ; c ) .
Đạo hàm f ' ( x ) = x x 2 + a 2 + x − c x 2 − 2 c x + b 2 + c 2 = 0
⇔ x x 2 − 2 c x + b 2 + c 2 = ( c − x ) x 2 + a 2 ⇔ x 2 c − x 2 + b 2 = c − x 2 x 2 + a 2
⇔ x 2 b 2 = c - x 2 a 2 ⇔ b x = ( c − x ) a ⇔ x = a c a + b ∈ ( 0 ; c ) .
Lập bảng biến thiên tìm ta được f(x) đạt nhỏ nhất khi x = a c a + b .
Cách 2: Dùng kiến thức hình học
Gọi D' là điểm đối xứng với D qua AB. Khi đó M C + M D = M C + M D ' ≥ C D ' . Do vậy ( M C + M D ) min = C D ' . Dấu = xảy ra khi M ∈ C D ' hay M = C D ' ∩ A B .
Khi đó Δ A M C ∽ △ B M D '
⇒ A M B M = A C B D ' ⇔ x c − x = a b ⇔ x = a c a + b