K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MB
1
MB
3
6 tháng 11 2021
\(\sqrt{2x+5}\) xác định khi \(2x+5\ge0\Rightarrow2x\ge-5\Rightarrow x\ge-\dfrac{5}{2}\)
6 tháng 11 2021
\(\sqrt{2x+5}\le0\Leftrightarrow2x+5\le0\Leftrightarrow2x\le-5\Leftrightarrow x\ge\dfrac{-5}{2}\)
\(\Rightarrow\) Đáp án: A
MB
2
6 tháng 11 2021
ĐKXĐ: \(2x-3\ge0\\ \Rightarrow2x\ge0+3\\ \Rightarrow2x\ge3\\ \Rightarrow x\ge\dfrac{3}{2}\left(A\right)\)
MB
4
6 tháng 11 2021
\(\sqrt{3-2x}\) xác định khi \(3-2x\ge0\Rightarrow2x\le3-0\Rightarrow2x\le3\Rightarrow x\le\dfrac{3}{2}\left(D\right)\)
BK
2
11 tháng 2 2020
a) ta có : \(\Delta'=\left(m-3\right)^2\ge0\forall m\)
==> phương trình lun có nghiệm với mọi m (đpcm)
b) \(x_1=\frac{-b'+\sqrt{\Delta}}{a}=m-2+\sqrt{\left(m-3\right)^2}=2m-5\)
\(x_1=\frac{-b'-\sqrt{\Delta}}{a}=m-2-\sqrt{\left(m-3\right)^2}=1\)
ta có : \(x_1\left(1-x_2\right)+x_2\left(1-x_1\right)< 4\Leftrightarrow x_1+x_2-2x_1x_2-4< 0\)
\(\Leftrightarrow2m-5+1-2\left(2m-5\right)-4< 0\Leftrightarrow m>1\)
vậy ......
BK
11 tháng 2 2020
Trần Thanh PhươngAkai HarumaMysterious PersonTrần Việt Linh@tth_new@Nguyễn Việt Lâm
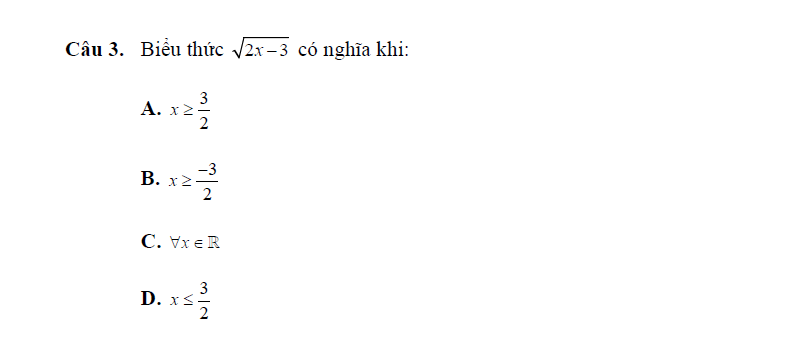
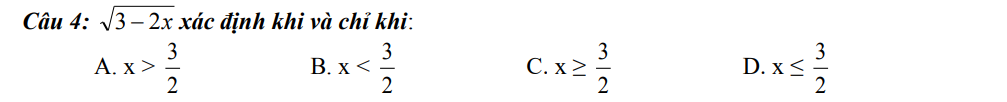
x<0
a<0