
 roi nha
roi nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 roi nha
roi nha

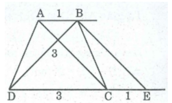
Phân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán
Từ B kẻ đường thẳng song song với AC cắt CD tại E. Tứ giác ABEC là hình thang có hai cạnh bên song song nên CE = AB = l cm, BE = AC = 3cm
Tam giác BDE xác định được, ta cần xác định đỉnh C và A.
- Đỉnh C nằm trên tia DE cách D một khoảng bằng 3cm
- Đỉnh A nằm trên đường thẳng đi qua B và song song với CD, A cách C một khoảng bằng 3 cm. (ABCD là hình thang cân nên AC = BD = 3 cm)
Cách dựng:
- Dựng ∆ BDE biết BD = 3cm, BE = 3cm , DE = 4cm
- Dựng điểm C trên tia DE sao cho DC = 3cm
- Dựng đường thẳng d đi qua B song song với CD.
- Dựng cung tròn tâm C bán kính 3 cm cắt đường thắng d tại A. Nối AD ta có hình thang ABCD dựng được.
Chứng minh: Thật vậy theo cách dựng ta có AB // CD.
Tứ giác ABCD là hình thang. CD = 3cm, AC = BD = 3cm. Vậy ABCD là hình thang cân thỏa mãn điều kiện bài toán.
Bài toán có một nghiệm hình.


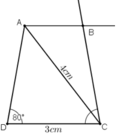
a) Phân tích
Giả sử dựng được hình thang ABCD theo yêu cầu đề bài.
Ta dựng được đoạn thẳng CD = 3cm.
Điểm A phải thỏa mãn hai điều kiện:
+ Tia DA tạo với DC một góc bằng 80º.
+ CA = 4cm nên A thuộc cung tròn tâm C bán kính 4cm.
ABCD là hình thang nên AB // CD
Hình thang ABCD cân nên 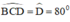
Vì vậy điểm B phải thỏa mãn 2 điều kiện:
+ B nằm trên đường thẳng đi qua A và song song với CD
+ Tia CB tạo với CD một góc 80º.
b) Cách dựng
+ Dựng đoạn CD = 3cm.
+ Dựng tia Dx thỏa mãn 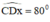
+ Dựng cung tròn tâm C, bán kính 4cm cắt tia Dx tại A.
+ Qua A dựng đường thẳng m song song với CD.
+ Dựng tia Cy trên cùng nửa mặt phẳng chứa điểm A, bờ CD thỏa mãn 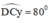
+ Tia Cy cắt đường thẳng m tại B.
Ta dựng được hình thang ABCD
c) Chứng minh
+ Tứ giác ABCD là hình thang vì AB // CD
+ Hình thang ABCD có 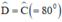 nên là hình thang cân.
nên là hình thang cân.
+ Hình thang cân ABCD có CD = 3cm, AC = 4cm, 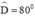 nên thỏa mãn yêu cầu đề bài.
nên thỏa mãn yêu cầu đề bài.
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện đề bài.

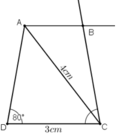
a) Phân tích
Giả sử dựng được hình thang ABCD theo yêu cầu đề bài.
Ta dựng được đoạn thẳng CD = 3cm.
Điểm A phải thỏa mãn hai điều kiện:
+ Tia DA tạo với DC một góc bằng 80º.
+ CA = 4cm nên A thuộc cung tròn tâm C bán kính 4cm.
ABCD là hình thang nên AB // CD
Hình thang ABCD cân nên 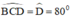
Vì vậy điểm B phải thỏa mãn 2 điều kiện:
+ B nằm trên đường thẳng đi qua A và song song với CD
+ Tia CB tạo với CD một góc 80º.
b) Cách dựng
+ Dựng đoạn CD = 3cm.
+ Dựng tia Dx thỏa mãn
+ Dựng cung tròn tâm C, bán kí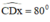 nh 4cm cắt tia Dx tại A.
nh 4cm cắt tia Dx tại A.
+ Qua A dựng đường thẳng m song song với CD.
+ Dựng tia Cy trên cùng nửa mặt phẳng chứa điểm A, bờ CD thỏa mãn 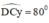
+ Tia Cy cắt đường thẳng m tại B.
Ta dựng được hình thang ABCD
c) Chứng minh
+ Tứ giác ABCD là hình thang vì AB // CD
+ Hình thang ABCD có 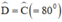 nên là hình thang cân.
nên là hình thang cân.
+ Hình thang cân ABCD có CD = 3cm, AC = 4cm, 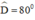 nên thỏa mãn yêu cầu đề bài.
nên thỏa mãn yêu cầu đề bài.
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện đề bài.

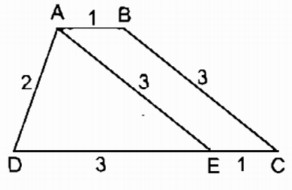
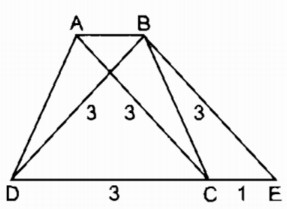
hân tích: Giả sử hình thang ABCD dựng được thỏa mãn điều kiện bài toán.
Qua A kẻ đường thẳng song song với BC cắt CD tại E ta thấy tam giác AED xác định vì biết ba cạnh, ta cần xác định đỉnh B và C
– Đỉnh C nằm trên tia DE, cách D một khoảng bẳng 4cm
– Đỉnh B nằm trên đường thẳng đi qua A song song với đường thẳng DE và cách A một khoảng bằng 1cm.
Cách dựng:
QUẢNG CÁO
– Dựng ∆ ADE biết AD = 2cm, DE = 3cm, AE = 3cm
– Trên tia DE dựng điểm C sao cho DC = 4cm
– Dựng đường thẳng đi qua A và song song với DC, lấy điểm B sao cho AB = 1cm. Nối BC ta có hình thang ABCD cần dựng
Chứng minh: Thật vậy theo cách dựng ta có AB // CD nên tứ giác ABCD là hình thang.
Ta có: AD = 2cm, DC = 4cm, AB = 1cm, hình thang ABCE có hai cạnh đáy AB = EC = 1cm nên BC = AE = 3cm.
Hình thang ABCD thỏa mãn điều kiện bài toán.
Biện luận: Tam giác ADE luôn dựng được nên hình thang ABCD dựng được, bài toán có một nghiệm hình.