Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

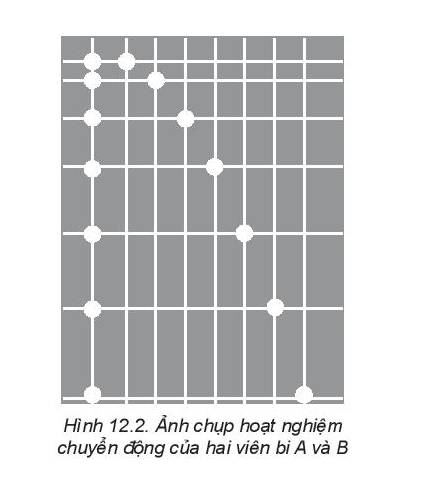
Thông qua quan sát, ta thấy tọa độ tính theo phương ngang của hai viên bi A và viên bi B đều không thay đổi, và đều trong cùng một khoảng thời gian
Mặt khác, ta có \(v=\dfrac{s}{t}=\dfrac{x}{t}\)
(do vật không đổi chiều chuyển động). Tọa độ x không đổi, thời gian như nhau, nên vận tốc không thay đổi
\(\Rightarrow v_x=v_0\)
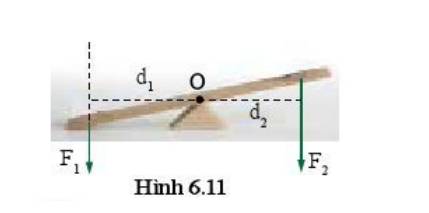
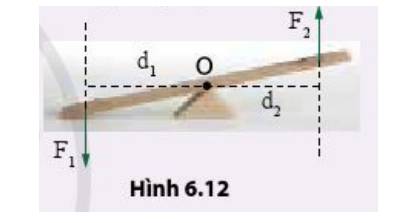
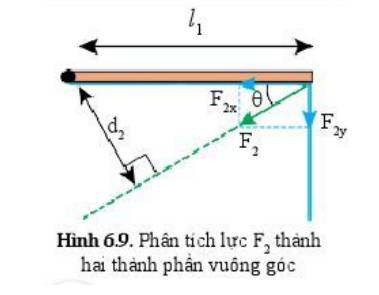
- Lực F1 có mômen lực là \(M_1=F_1d_1\) và có tác dụng làm vật quay ngược chiều kim đồng hồ.
- Lực F2 có mômen lực là \(M_2=F_2d_2\) và có tác dụng làm vật quay cùng chiều kim đồng hồ.
⇒ Điều kiện cân bằng của vật có trục quay cố định là mômen lực có xu hướng làm vật quay ngược chiều kim đồng hồ bằng với mômen lực có xu hướng làm vật quay theo chiều kim đồng hồ.

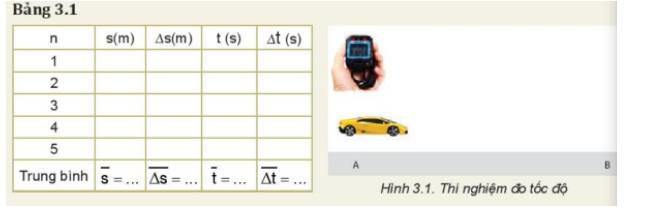
a) Nguyên nhân gây ra sự sai khác giữa các lần đo là:
- Do đặc điểm và cấu tạo của dụng cụ đo
- Do điều kiện làm thí nghiệm chưa được chuẩn
- Do thao tác khi đo
b) Ta có:
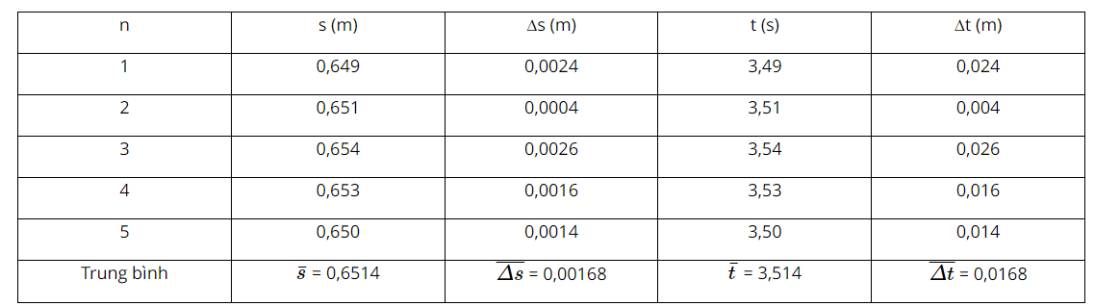
\(\overline {\Delta s} = \frac{{\left| {\overline s - {s_1}} \right| + \left| {\overline s - {s_2}} \right| + ... + \left| {\overline s - {s_5}} \right|}}{5} = 0,00168\)
\(\overline {\Delta t} = \frac{{\left| {\overline t - {t_1}} \right| + \left| {\overline t - {t_2}} \right| + ... + \left| {\overline t - {t_5}} \right|}}{5} = 0,0168\)
c) Viết kết quả đo:
Ta có:
\(\Delta s = \overline {\Delta s} + \Delta {s_{dc}} = 0,00168 + \frac{{0,001}}{2} = 0,00218\)
\(\Delta t = \overline {\Delta t} + \Delta {t_{dc}} = 0,0168 + \frac{{0,01}}{2} = 0,0218\)
Suy ra:
\(s = \overline s \pm \Delta s = 0,6514 \pm 0,00218\left( m \right)\)
\(t = \overline t \pm \Delta t = 3,514 \pm 0,0218\left( s \right)\)
d) Tính sai số tỉ đối:
\(\delta t = \frac{{\Delta t}}{{\overline t }}.100\% = \frac{{0,0218}}{{3,514}}.100\% = 0,620\)
\(\delta s = \frac{{\Delta s}}{{\overline s }}.100\% = \frac{{0,00218}}{{0,6514}}.100\% = 0,335\)
\(\delta v = \frac{{\Delta s}}{{\overline s }}.100\% + \frac{{\Delta t}}{{\overline t }}.100\% = 0,335 + 0,620 = 0,955\)
\(\Delta v = \delta v.\overline v = 0,955.\frac{{0,6514}}{{3,514}} = 0,177\left( {m/s} \right)\)

1.
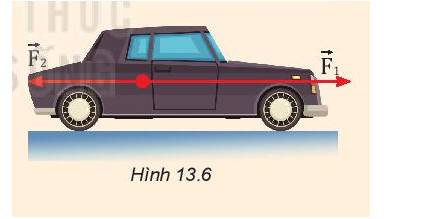
Ta thấy: \(\overrightarrow {{F_1}} \uparrow \downarrow \overrightarrow {{F_2}} \Rightarrow F = \left| {{F_1} - {F_2}} \right| = \left| {400 - 300} \right| = 100N\)
Và có chiều hướng về phía trước.
2.
a)
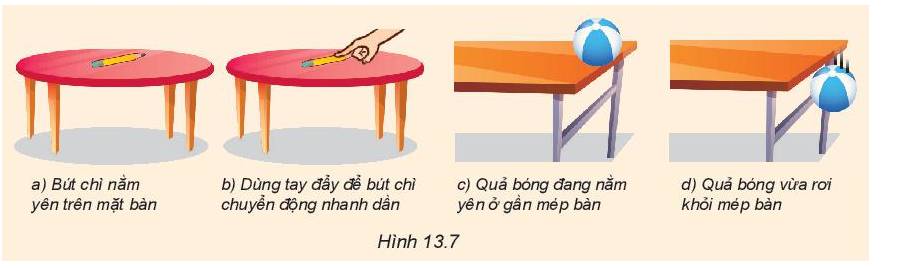
Tình huống có hợp lực khác 0 là:
- Dùng tay đẩy để bút chì chuyển động nhanh dần
- Qủa bóng vừa rơi khỏi mép bàn.
b)
- Dùng tay đẩy để bút chì chuyển động nhanh dần: độ lớn vận tốc sẽ tăng dần, hướng chuyển động về phía trước.
- Quả bóng vừa rơi khỏi mép bàn: độ lớn vận tốc tăng dần, hướng chuyển động theo phương thẳng đứng hướng xuống.

a) gọi t là thời điểm 2 xe gặp nhau
phương trình chuyển động của xe 1 và xe 2 lần lượt là :
x1 = 60t
x2 = 120 - 40t
b) 0 0,5 1 t (h) x(km) 20 40 60 80 100 120 x1 x2 1,2 72
c) vì 2 xe gặp nhau nên x1 = x2
=> 120-40t = 60t
=> t = 1,2(h)
nơi gặp nhau cách A : S = x1 =60t = 60.1,2 = 72 (km)
xét đồ thì thấy đúng vs kết quả
d) tọa độ của 2 xe sau 2 h lần lượt là :
x1' = 60t = 60.2 = 120 (km)
x2' = 120 - 40t = 120 - 40.2 = 40 (km)
khoảng cách 2 xe là : x1' - x2' = 120 - 40 = 80 (km)

Tham khảo:
- Giai đoạn 1 (từ 0 – t1): đồ thị là một đoạn rất nhỏ có dạng gần giống như đường thẳng chứng tỏ vận tốc của vật tăng đều theo thời gian. Có thể kết luận vật rơi nhanh dần đều từ lúc bắt đầu rơi trong một thời gian rất ngắn.
- Giai đoạn 2 (từ t1 – t2): đồ thị là một đoạn đường cong đi lên chứng tỏ vận tốc có tăng nhưng không đều. Có thể kết luận vật rơi nhanh dần không đều trong một khoảng thời gian tiếp theo, lúc này lực cản bắt đầu có độ lớn đáng kể và tăng dần.
- Giai đoạn 3 (từ t2 trở đi): đồ thị có dạng gần như một đường thẳng nằm ngang song song với trục thời gian chứng tỏ tốc độ chuyển động không đổi. Có thể kết luận vật rơi trong giai đoạn này như là một chuyển động đều với tốc độ giới hạn không đổi, khi đó lực tác dụng lên vật rơi bị triệt tiêu.
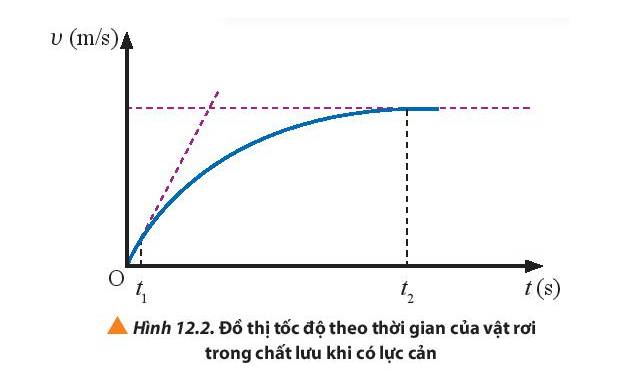

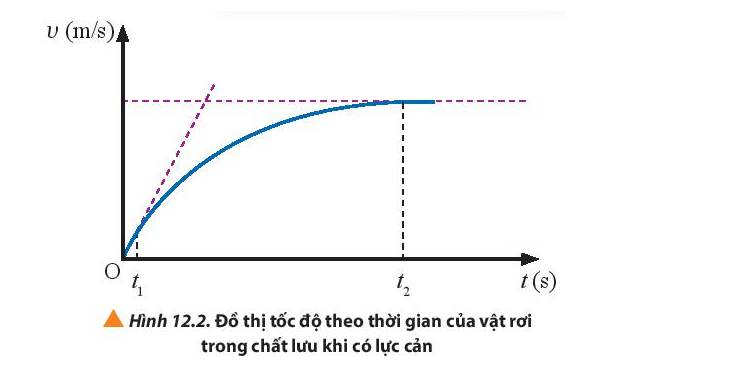
Từ đồ thị trong Hình 12.2, ta có:
+ Từ 0 – t1, vật chuyển động nhanh dần đều.
+ Từ t1 – t2, vật chuyển động nhanh dần không đều.
+ Từ t2 trở đi, vật chuyển động với tốc độ không đổi.