Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo giả thiết ta vẽ được hình:

Khi đó AN = AM + MN và AB = AN + NB.
Suy ra AB = (AM + MN) + NB
Do AM = NB = 2 cm nên 10 = 2 + MN + 2.
Từ đó tính được MN = 10 - 4 = 6 (cm)


Từ giả thiết AB = 12cm và điểm N nằm giữa hai điểm A, B sao cho AN = 2cm
Suy ra: AN + NB = AB
Thay số 2 + NB = 12 nên NB = 10 cm
M là trung điểm của đoạn thẳng BN nên BM = MN = 5cm.
Cũng do MN = 5cm và P là trung điểm của đoạn thẳng MN nên NP = PM = 2,5cm. Từ đó, ta có thể vẽ được hình như sau

* Trên tia NB có NP < NB (do 2,5cm < 10cm) nên điểm P nằm giữa hai điểm N và B.
Do đó: BN = NP + BP
Suy ra BP = BN - NP = 10 - 2,5 = 7,5 cm

Câu đúng: e), f), g).
Câu sai: a), b), c), d).
Điểm M được gọi là trung điểm của đoạn thẳng AB nếu M nằm giữa A, B và cách đều hai điểm đó (AM = MB).
* Câu a còn thiếu điều kiện là MA = MB.
* Câu b sai vì thiếu điều kiện M nằm giữa A và B.
* Câu c thiếu điều kiện MA = MB.
* Câu d thiếu điều kiện 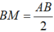

Theo đầu bài cho trên tia AB nghĩa là lấy A làm gốc,lấy điểm M,N để AM=3cm,AN=6cm có thể suy ra M nằm giữa A,N.
MN=AN-AM=6-3=3cm
NB=AB-AN=8-6=2cm
vậy MN=3cm,NB=2cm
Theo phần đầu M nằm giữa A,N.mà AM=MN=3cm vậy M nằm giữa và cách đều A,N.Vậy M là trung điểm của AN

A B C D
a) Ta có: \(\hept{\begin{cases}AC+BD=9cm\\AD+BD=6cm\end{cases}}\)
\(\Rightarrow AC-AD=3cm\)hay \(AD< AC\)
Suy ra D nằm giữa A và C.(đpcm)(1)
b) Từ (1) suy ra AD + DC = AC
hay CD = AC - AD
\(\Leftrightarrow CD=3cm\)
Vậy CD = 3cm
trongtruong72 hợp a)
+ M nằm giữa A và N nên : AM + MN = AN => AM = AN - NM
+ M nằm giữa M và B nên |: BN + NM = BM => BN = BM - NM
vì AN = BM , MN nên AM = BN
trong trường hợp b)
+ N nằm giữa A và M nên AN + NM = AM
+ M nằm giữa N và B nên BM + MN = BN
Vì AN = BM , MN = NM nên AM = BN
- Vì \(M\) nằm giữa \(A\) và \(M\) nên \(AN=AM+MN\) (1)
- Vi \(N\) nằm giữa \(B\) và \(M\) nên \(BM=BN+MN\) (2)
Mà \(AN=BM\) ( đề bài ) nên từ (1) và (2) suy ra \(AM+MN=BN+MN\)
Do đó : \(AM=BN\)
- Vì \(N\) nằm giữa \(A\) và \(M\) nên \(AN+NM=AM\) (3)
- Vì \(M\) nằm giữa \(B\) và \(N\) nên \(BM+MN=BN\) (4)
Mà \(AN=BM\) (đề bài) nên từ (3) và (4) nên \(AM=BN\)