Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

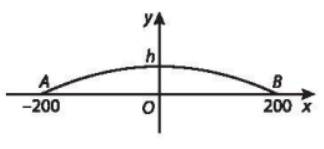
Chọn hệ trục tọa độ Oxy sao cho O là trung điểm AB, tia Ox trùng với tia OB, tia Oy hướng lên trên.
Khi đó \(A\left(-200;0\right),B\left(200;0\right)\). Gọi chiều cao giới hạn của cầu là h (h > 0), suy ra đỉnh cầu có tọa độ (0;h)
Ta tìm được phương trình parabol của cầu là: \(y=-\dfrac{h}{200^2}\cdot x^2+h\)
Ta có: \(y'=-\dfrac{2h}{200^2}\cdot x\), suy ra hệ số góc xác định độ dốc của mặt cầu là
\(k=y'=-\dfrac{2h}{200^2}\cdot x;-200\le x\le200\)
Vì độ dốc của mặt cầu không quá 10o nên ta có: \(\dfrac{h}{100}\le tan10^o\Leftrightarrow h\le17,6\)
Vậy chiều cao giới hạn từ đỉnh cầu tới mặt đường là 17,6cm

Giả sử góc tạo bởi đường thẳng dành cho người khuyết tật và mặt phẳng nằm ngang là α
Vì độ dốc của đường thẳng dành cho người khuyết tật được quy định là không quá \(\frac{1}{{12}}\)nên ta có
\(\tan \alpha \le \frac{1}{{12}} \Rightarrow \alpha \le 4,{76^0}\)
Vậy góc tạo bởi đường dành cho người khuyết tật và mặt phẳng nằm ngang không vượt quá 4,760

Gọi B là một điểm nằm trên thanh ngang và H là hình chiếu vuông góc xuống mặt dốc.
Vì dốc nghiêng 150 so với phương nằm ngang nên nên góc giữa cột và mặt phẳng dốc bằng 750
Khoảng cách từ B đến mặt phẳng dốc là:
\(BH=2.28\cdot sin75\simeq2,2\left(m\right)\)
=>Không cho phép xe cao 2,21m đi qua cầu

a, Vì gốc tọa độ đặt tại P nên P(0;0) do đó ta có \(c=y\left(0\right)=0\)
b, \(y'=2ax+b\Rightarrow y'\left(0\right)=b\)
Mà L1 là phương trình tiếp tuyến tại P có hệ số góc là 0,5 nên \(y'\left(0\right)=0,5\Rightarrow b=0,5\)
c, L2 là phương trình tiếp tuyến tại Q có hệ số góc -0,75 nên \(y'\left(x_Q\right)=2ax_Q+0,5=-0,75\)
Vì khoảng cách theo phương ngang giữa P và Q là 40m nên \(x_Q-x_P=x_Q=40\)
\(\Rightarrow2a\cdot40+0,5=-0,75\\ \Leftrightarrow a=-\dfrac{1}{64}\)
d, \(y_Q=-\dfrac{1}{64}\cdot40^2+0,5\cdot40=-5\)
Vậy chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q là \(\left|y_P-y_Q\right|=5\)

Chọn B
Lời giải. Không gian mẫu là số cách chọn 2 điểm bất kỳ trong 14 điểm đã cho.
Suy ra số phần tử của không gian mẫu là Ω = C 14 2 = 91 .
Gọi A là biến cố :
Đoạn thẳng nối 2 điểm được chọn cắt hai trục tọa độ.
Để xảy ra biến cố A thì hai đầu đoạn thẳng đó phải ở góc phần tư thứ nhất và thứ ba hoặc phần tư thứ hai và thứ tư.
● Hai đầu đoạn thẳng ở góc phần tư thứ nhất và thứ ba, có C 2 1 . C 4 1 cách.
● Hai đầu đoạn thẳng ở góc phần tư thứ hai và thứ tư, có C 3 1 . C 5 1 cách.
Suy ra số phần tử của biến cố A là
Ω A = C 2 1 . C 4 1 + C 3 1 . C 5 1 =23
Vậy xác suất cần tính
P ( A ) = Ω A Ω = 23 91

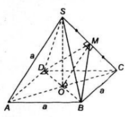
a) Theo giả thiết, S.ABCD là hình chóp đều và đáy ABCD là hình vuông nên SO ⊥ (ABCD) ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
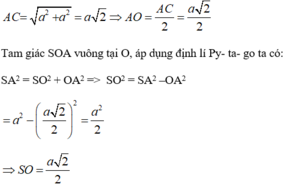

=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45 o





Mô hình hoá như hình vẽ, với \(AB\) là chiều dài con dốc, \(AH\) là độ cao của điểm \(A\) so với mặt nước biển, \(BK\) là độ cao của điểm \(B\) so với mặt nước biển, \(BI\) là chiều cao của con dốc, độ lớn của góc \(\widehat {BAI}\) chỉ độ dốc.
Ta có: \(AH = 200,BK = 220,AB = 120\).
\(AHKB\) là hình chữ nhật \( \Rightarrow IK = AH = 200 \Rightarrow BI = BK - IK = 220 - 200 = 20\)
Vì tam giác \(ABI\) vuông tại \(I\) nên ta có:
\(\sin \widehat {ABI} = \frac{{BI}}{{AB}} = \frac{{20}}{{120}} = \frac{1}{6} \Rightarrow \widehat {ABI} \approx 9,{59^ \circ }\) tương ứng với 10,66%
Vậy độ dốc của con dốc đó là 10,66%.