Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a)
Hàm $y$ đồng biến trên khoảng xác định khi mà
\(y'=3x^2-6(2m+1)x+12m+5\geq 0\)
\(\Leftrightarrow \Delta'=9(2m+1)^2-3(12m+5)\leq 0\)
\(\Leftrightarrow -\sqrt{\frac{1}{6}}\leq m\leq \sqrt{\frac{1}{6}}\)
b) Hàm $y$ đồng biến trên TXĐ khi:
\(y'=3mx^2-2(2m-1)x+m-2\geq 0\) với mọi \(x\in\mathbb{R}\)
Để đảm bảo điều trên xảy ra với mọi $x$ thì \(m>0\)
Khi đó \(\Delta'=(2m-1)^2-3m(m-2)\leq 0\)
\(\Leftrightarrow (m+1)^2\leq 0\) (vô lý)
Do đó không tồn tại $m$ thỏa mãn

\(y'=x^2-2\left(m+1\right)x+m\)
Hàm đồng biến trên \(\left[4;9\right]\Leftrightarrow y'\ge0\) với mọi \(x\in\left[4;9\right]\)
\(\Leftrightarrow x^2-2\left(m+1\right)x+m\ge0\)
\(\Leftrightarrow x^2-2x\ge m\left(2x-1\right)\)
\(\Leftrightarrow m\le\frac{x^2-2x}{2x-1}\Rightarrow m\le\min\limits_{\left[4;9\right]}f\left(x\right)\) với \(f\left(x\right)=\frac{x^2-2x}{2x-1}\)
\(f'\left(x\right)=\frac{2\left(x^2-x+1\right)}{\left(2x-1\right)^2}>0\) \(\forall x\in\left[4;9\right]\Rightarrow f\left(x\right)_{min}=f\left(4\right)=\frac{8}{7}\Rightarrow m\le\frac{8}{7}\)

đáp án:
Hàm số đã cho xác định trên D = R.
Với m = -1. Khi đó hàm số trở thành y = -2x + 4 ; y' = -2 < 0 ∀x∈R, không thỏa mãn yêu cầu bài toán.
Với m ≠ -1. Ta có f'(x)= 3(m+1)x2 - 6(m + 1)x + 2m
+ Hàm số đồng biến trên khoảng có độ dài không nhỏ hơn 1 khi và chỉ khi f'(x) = 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn [x1;x2 ] thỏa mãn |x1 - x2 | ≥ 1
+ f'(x)= 0 có hai nghiệm phân biệt x1,x2 và hàm số đồng biến trong đoạn[x1;x2]
Theo Viét ta có
+ Với |x1 - x2 | ≥ 1 ⇔ (x1 + x2 )2 - 4x1 x2 - 1 ≥ 0
Đối chiếu điều kiện ta có m ≤ -9.

\(y'=f\left(x\right)=6x^2-2mx+2\) (1)
Để hàm số đồng biến trên \(\left(-2;0\right)\Leftrightarrow f\left(x\right)\ge0\) ; \(\forall x\in\left(-2;0\right)\)
\(\Leftrightarrow6x^2+2\ge2mx\Leftrightarrow\frac{3x^2+1}{x}\le m\Leftrightarrow m\ge\max\limits_{\left(-2;0\right)}\frac{3x^2+1}{x}\)
Xét \(g\left(x\right)=\frac{3x^2+1}{x}\Rightarrow g'\left(x\right)=\frac{3x^2-1}{x^2}=0\Rightarrow x=-\frac{1}{\sqrt{3}}\)
Từ BBT ta thấy \(\max\limits_{\left(-2;0\right)}g\left(x\right)=g\left(-\frac{1}{\sqrt{3}}\right)=-2\sqrt{3}\)
\(\Rightarrow m\ge-2\sqrt{3}\)

- Với \(m=0\) thỏa mãn
- Với \(m\ne0\Rightarrow y'=f\left(x\right)=3mx^2-2x+3\)
Để hàm số đồng biến trên \(\left(-3;0\right)\Leftrightarrow f\left(x\right)\ge0\) ; \(\forall x\in\left(-3;0\right)\)
\(\Leftrightarrow3mx^2-2x+3\ge0\Leftrightarrow3m\ge\frac{2x-3}{x^2}\)
\(\Leftrightarrow3m\ge\max\limits_{\left(-3;0\right)}\frac{2x-3}{x^2}\)
Xét \(g\left(x\right)=\frac{2x-3}{x^2}\Rightarrow g'\left(x\right)=\frac{6-2x}{x^3}< 0\) ; \(\forall x\in\left(-3;0\right)\)
\(\Rightarrow g\left(x\right)\) nghịch biến \(\Rightarrow g\left(x\right)< g\left(-3\right)=-1\)
\(\Rightarrow3m\ge-1\Leftrightarrow m\ge-\frac{1}{3}\)

ta có
\(y'=3x^2-6x=3x\left(x-2\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
y' >0 khi \(x\in\left(-\infty,0\right)\cup\left(2,+\infty\right)\)
Vậy hàm đồng biến trên hai khoảng là \(\left(-\infty,0\right)\cup\left(2,+\infty\right)\)

\(y'=x^2+2\left(m+1\right)x-\left(m+1\right)\)
Hàm đồng biến trên R khi và chỉ khi \(y'\ge0\) ; \(\forall x\in R\)
\(\Leftrightarrow x^2+2\left(m+1\right)x-\left(m+1\right)\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=\left(m+1\right)^2+\left(m+1\right)\le0\)
\(\Leftrightarrow\left(m+1\right)\left(m+2\right)\le0\)
\(\Leftrightarrow-2\le m\le-1\)

a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3
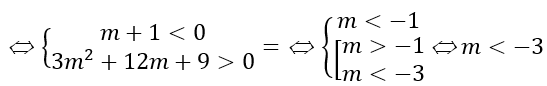
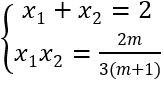
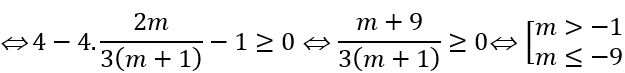

1+1=2