Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

'''''''''''''F'F'S'JURSMJHYT,JTHDNHTDNMYHJFGJHTMJHTMJYT

a) * Lớp 10C:

* Lớp 10D:

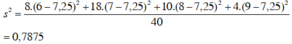
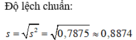
b) Kết quả lớp 10D có độ lệch chuẩn nhỏ hơn kết quả lớp 10C nên kết quả lớp 10D đồng đều hơn.

a) Ta có: \(8 - 7 = 1;6 - 7 = - 1;7 - 7 = 0;5 - 7 = - 2;9 - 7 = 2\)
b) +) Bình phương các độ lệch là: \({(8 - 7)^2} = 1;{(6 - 7)^2} = 1;{(7 - 7)^2} = 0;{(5 - 7)^2} = 4;{(9 - 7)^2} = 4\)
+) Trung bình cộng của bình phương các độ lệch là:
\({s^2} = \frac{{{{(8 - 7)}^2} + {{(6 - 7)}^2} + {{(7 - 7)}^2} + {{(5 - 7)}^2} + {{(9 - 7)}^2}}}{5} = 2\)

Số trung bình cộng của mẫu số liệu trên là: \(\overline X = \frac{{1 + 1 + 3 + 6 + 7 + 8 + 8 + 9 + 10}}{9} \approx 5,9\)
Nhận xét: Quan sát mẫu số liệu trên, ta thấy nhiều số liệu có sự chênh lệch lớn so với số trung bình cộng. Vì vậy, ta không thể lấy số trung bình cộng làm đại diện cho mẫu số liệu mà ta phải chọn số đặc trưng khác thích hợp hơn.

Cách 1. Ta có: Khi cộng vào mỗi số liệu của một dãy số liệu thống kê cùng một hằng số thì phương sai và độ lệch chuẩn không thay đổi. Do đó độ lệch chuẩn của dãy (2) vẫn là 2 kg.
Cách 2. Tính trực tiếp độ lệch chuẩn của dãy (2).
Đáp án: A.

Sắp xếp lại:
5 | 31 | 37 | 43 | 43 | 57 | 62 | 63 | 78 | 80 | 91 |
Khoảng biến thiên R=91-5=86
Ta có: \({Q_2} = 57,{Q_1} = 37,{Q_3} = 78\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 78 - 37 = 41\)
Số trung bình \(\overline X \approx 53,64\)
Ta có bảng sau:
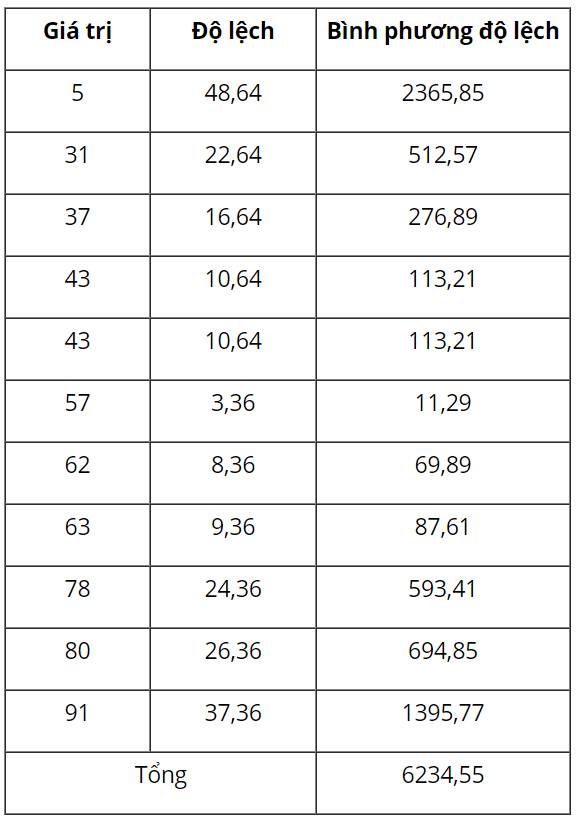
Độ lệch chuẩn là 79
Môn Tiếng Anh:
Sắp xếp lại:
37 | 41 | 49 | 55 | 57 | 62 | 64 | 65 | 65 | 70 | 73 |
Khoảng biến thiên R=73-37=36
Ta có: \({Q_2} = 62,{Q_1} = 49,{Q_3} = 65\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 65 - 49 = 16\)
Số trung bình \(\overline X = 58\)
Ta có bảng sau:
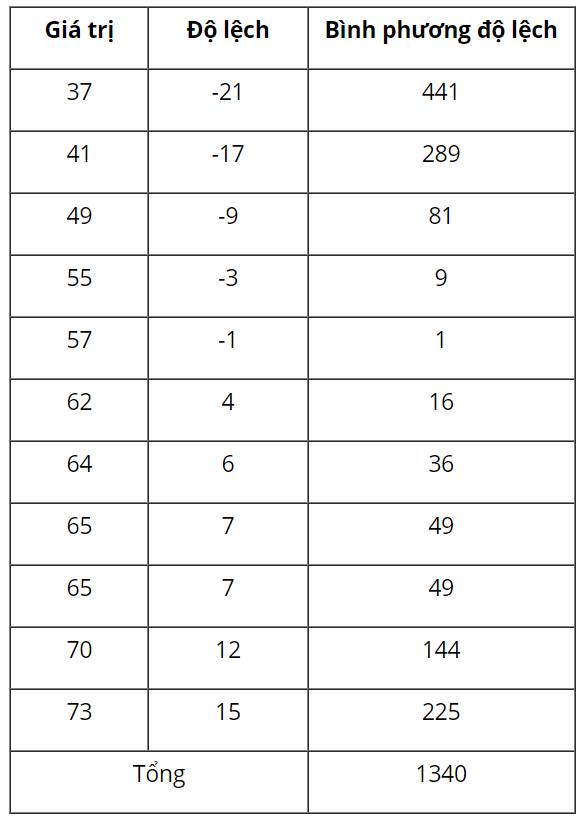
Độ lệch chuẩn là 36,6
Từ các số trên ta thấy mức độ học tập môn Tiếng Anh không đều bằng môn Toán.Độ lệch chuẩn là 36,6

Sắp xếp lại theo thứ tự không giảm:
Bạn An: 6,5 6,8 7,3 8,0 8,0 8,7 9,2 9,5
Bạn Bình: 7,6 7,8 7,9 8,0 8,1 8,1 8,2 8,3
+ So sánh theo khoảng biến thiên:
Bạn An: \({R_1} = 9,5 - 6,5 = 3\)
Bạn Bình: \({R_2} = 8,3 - 7,6 = 0,7\)
Ta thấy \({R_1} > {R_2}\) nên bạn Bình học đều hơn
+ So sánh theo khoảng tứ phân vị:
Bạn An: n=8
\({Q_1} = \frac{{6,8 + 7,3}}{2} = 7,05\), \({Q_4} = \frac{{8,7 + 9,2}}{2} = 8,95\)
Khoảng tứ phân vị là \({\Delta _Q} = {Q_3} - {Q_1} = 8,95 - 7,05 = 1,9\)
Bạn Bình: n=8
\(Q{'_1} = \frac{{7,8 + 7,9}}{2} = 7,85\), \(Q{'_3} = \frac{{8,1 + 8,2}}{2} = 8,15\)
Khoảng tứ phân vị
\(\Delta {'_Q} = Q{'_3} - Q{'_1} = 8,15 - 7,85 = 0,3\)
=> Ta thấy \({\Delta _Q} > \Delta {'_Q}\) nên bạn Bình học đều hơn
+ So sánh theo phương sai hoặc độ lệch chuẩn
Bạn An: \(\overline x = 8\)
Ta có bảng:
Giá trị | Độ lệch | Bình phương độ lệch |
6,5 | -1,5 | 2,25 |
6,8 | -1,2 | 1,44 |
7,3 | -0,7 | 0,49 |
8 | 0 | 0 |
8 | 0 | 0 |
8,7 | 0,7 | 0,49 |
9,2 | 1,2 | 1,44 |
9,5 | 1,5 | 2,25 |
Tổng | 8,36 |
Phương sai là \({s_1}^2 = \frac{{8,36}}{8} = 1,045\)
Độ lệch chuẩn là \({s_1} = \sqrt {1,045} \approx 1,02\)
Bạn Bình: \(\overline x = 8\)
Ta có bảng:
Giá trị | Độ lệch | Bình phương độ lệch |
7,60 | -0,40 | 0,16 |
7,80 | -0,20 | 0,04 |
7,90 | -0,10 | 0,01 |
8,00 | 0,00 | 0,00 |
8,10 | 0,10 | 0,01 |
8,10 | 0,10 | 0,01 |
8,20 | 0,20 | 0,04 |
8,30 | 0,30 | 0,09 |
Tổng | 0,36 |
Phương sai là \({s_2}^2 = \frac{{0,36}}{8} = 0,045\)
Độ lệch chuẩn là \({s_2} = \sqrt {0,045} \approx 0,21\)
Ta thấy \({s_2} < {s_1}\) nên bạn Bình học đều hơn

a) Số trung bình điểm thi Ngữ văn của lớp 10C và 10D tương ứng là
.(3x5 + 7x6 + 12x7 + 14x8 + 3x9 + 1x10) = 7,25
.(8x6+18x7+10x8+4x9) = 7,25.
Phương sai bảng điểm thi Văn của hai lớp theo thứ tự là:
= 1,2875
= 0,7875.
Độ lệch chuẩn theo thứ tự là Sx ≈ 1,1347 Sy ≈ 0,8874.
b) Qua xem xét các số đặc trung ta thấy điểm trung bình thi văn 2 lớp 10C và 10D là như nhau (đều bằng 7,25). Nhưng phương sai của bảng điểm thi lớp 10D nhỏ hơn phương sai tương ứng ở lớp 10C. Điều đó chứng tỏ kết quả làm bài thi Văn ở lớp 10D đồng đều hơn.

Ví dụ, ta có bảng đo chiều cao của các bạn trong tổ như sau:
160 | 162 | 164 | 165 | 172 | 174 | 177 | 178 | 180 |
a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
160 162 164 165 172 174 177 178 180
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{160\;\; + 162\;\; + 164\;\;\; + \;\;165\;\; + \;172\;\; + \;174\;\; + \;177\; + \;\;178\; + \;180}}{9} = \frac{{1532}}{9}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 9 số liệu ( lẻ ) nên trung vị \({Q_2} = 172\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 160 162 164 165 là: \({Q_1} = 163\)
- Trung vị của dãy 174 177 178 180 là: \({Q_3} = 177,5\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 163\), \({Q_2} = 172\), \({Q_3} = 177,5\)
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 180 - 160 = 20\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 177,5 - 163 = 14,5\)
c) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {160 - \overline x } \right)}^2} + {{\left( {162 - \overline x } \right)}^2} + ... + {{\left( {180 - \overline x } \right)}^2}} \right]}}{9} \approx 50,84\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 7,13\)


Trung vị tăng 0,5. Tứ phân vị cũng tăng 0,5.
Khi cộng thêm mỗi môn 0,5 điểm chuyên cần thì điểm trung bình tăng 0,5
=> Độ lệch của mỗi giá trị so với số trung bình vẫn không đổi \(\left( {{x_i} - \overline x} \right)\)
=> Độ lệch chuẩn không thay đổi.
Chọn C.