Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
- Giả sử nhiệt độ của hỗn hợp sau khi cân bằng là 0 0 C
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
![]()
- Ta thấy Q t h u < Q t ỏ a chứng tỏ nước đá bị tan ra hoàn toàn.
- Gọi nhiệt độ hỗn hợp sau khi cân bằng là t 0 C (t > 0)
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0 0 C , tan hết tại 0 0 C và tăng lên đến t 0 C là:
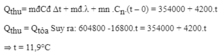

Đáp án: B
- Nhiệt lượng do xô và nước toả ra để hạ nhiệt độ xuống 0°C là:
![]()
- Nhiệt lượng thu vào của 1 viên nước đá để tăng nhiệt độ lên 0°C và tan hết tại 0°C là:
![]()
- Số viên nước đá cần phải thả vào nước là:
705000 : 83760 = 8,4
- Vậy phải thả vào xô ít nhất 9 viên đá để nhiệt độ cuối cùng trong xô là 0 0 C

Đáp án: D
- Nhiệt lượng do nước đá thu vào để tan chảy hoàn toàn ở 0°C là:
![]()
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0°C là:
![]()
- Ta thấy Q t h u > Q t ỏ a chứng tỏ chỉ 1 phần nước đá bị tan ra.
- Như vậy khi cân bằng nhiệt, hỗn hợp gồm cả nước và nước đá.
- Hay khi cân bằng nhiệt, nhiệt độ của hỗn hợp là t = 0 0 C

Tóm tắt:
m1 = 200g = 0,2kg ; c1 = 460J/kg.K
m2 = 500g = 0,5kg ; c2 = 880J/kg.K
V3 = 2l = 2.10-3m3 ; c3 = 4200J/kg.K
t23 = 20oC ; t = 28oC
a) Gọi nhiệt độ ban đầu của thỏi sắt (chính bằng nhiệt độ lò) là t1. Nhiệt lượng thỏi sắt tỏa ra đến khi cân bằng nhiệt là:
\(Q_1=m_1.c_1\left(t_1-t\right)=0,2.460\left(t_1-28\right)=92t_1-2576\)
Khối lượng của nước trong bình nhôm là: \(m_3=D_n.V_3=1000.2.10^{-3}=2\left(kg\right)\)
Nhiệt lượng bình nước thu vào đến khi cân bằng nhiệt là:
\(Q_2=\left(m_2.c_2+m_3.c_3\right)\left(t-t_{23}\right)=\left(0,5.880+2.4200\right)\left(28-20\right)=70720\left(J\right)\)
Ở phần này ta bỏ qua sự trao đổi nhiệt với môi trường nên theo phương trình cân bằng nhiệt:
\(Q_1=Q_2\Rightarrow92t_1-2576=70720\\ \Rightarrow92t_1=73296\\ \Rightarrow t_1\approx796,7\left(^oC\right)\)
Vậy nhiệt độ của lò là 796,7oC.
b) Có 10% nhiệt lượng của thỏi sắt bị tỏa ra ngời nên nhiệt lượng thỏi sắt truyền cho bình nước chỉ là 90%. Gọi t1' là nhiệt độ thực của thỏi sắt.
Nhiệt lượng thực tế mà thỏi sắt tỏa ra là:
\(Q_1'=\dfrac{Q_2}{H}=\dfrac{70720}{0,9}\approx78577,78\left(J\right)\)
Ta có:
\(Q_1'=m_1.c_1\left(t_1'-t\right)\\ \Rightarrow t_1'=\dfrac{Q_1'}{m_1.c_1}-t=\dfrac{78577,78}{0,2.460}+28\approx882,11\left(^oC\right)\)
Vậy thực tế lò nung có nhiệt độ là 882,11oC

Ta có phương trình cân bằng nhiệt
\(Q_{toả}=Q_{thu}\\ \Leftrightarrow0,3.460+0,4.380\left(25-t_{cb}\right)=0,2.4200\left(t_{cb}-20\right)\\ \Leftrightarrow t_{cb}=20,9^o\approx21^o\)

Đáp án: A
- Nhiệt lượng do chậu và nước toả ra để hạ nhiệt độ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của khối nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
![]()
- Vì Q 2 > Q 1 nên khối nước đá chưa tan hết

Đáp án: B
- Nhiệt lượng do cốc và nước toả ra để hạ nhiệt độ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của khối nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
![]()
- Vì Q 1 > Q 2 nên khối nước đá đã tan hết và nhiệt độ hỗn hợp lớn hơn 0 0 C
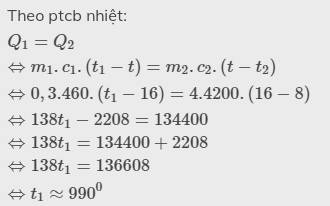
Theo ptcb nhiệt:
\(Q_1=Q_2\\ \Leftrightarrow m_1.c_1.\left(t_1-t\right)=m_2.c_2.\left(t-t_2\right)\\ \Leftrightarrow0,3.460.\left(t_1-16\right)=4.4200.\left(16-8\right)\\ \Leftrightarrow138t_1-2208=134400\\ \Leftrightarrow138t_1=134400+2208\\ \Leftrightarrow138t_1=136608\\ \Leftrightarrow t_1\approx990^0\)