Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
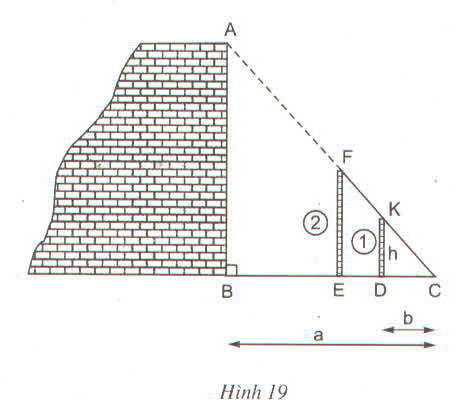
- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A,F,K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất( 3 điểm F,K,C thẳng hàng).
b) ∆BC có AB // EF nên EFABEFAB = ECBCECBC => AB = EF.BCECEF.BCEC = h.abh.ab
Vậy chiều cao của bức tường là: AB = h.abh.ab.
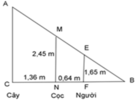
Ta mô tả vị trí cây, cọc và người như hình vẽ bên.
Xét ΔBFE và ΔBNM ta có:
B chung
B E F ^ = B M N ^ (vì EF // MN, cặp góc đồng vị bằng nhau)
=> ΔBFE ~ ΔBNM (g - g)
⇒ B F B N = F E N M ⇔ B F B F + F N = F E N M ⇔ B F B F + 0 , 64 = 1 , 65 2 , 45
⇔ 1,65(BF + 0,64) = 2,45.BF
⇔ BF = 1,32m
Xét ΔBFE và ΔBCA có:
B chung
B E F ^ = B A C ^ (vì EF // AC, cặp góc đồng vị bằng nhau)
=> ΔBFE ~ ΔBCA (g - g)
⇒ B F B C = F E C A ⇔ B F B F + F N + N C = F E C A ⇔ 1 , 32 1 , 32 + 0 , 64 + 1 , 36 = 1 , 65 C A
=> CA = 4,15m
Vậy cây cao đúng bằng độ dài của đoạn CA hay cây cao 4,15m.
Đáp án: D
Đặt tên các điểm như hình vẽ.
Ta có \(AB=0,8\left(m\right)\), \(BD=15\left(m\right)\), \(BC=2\left(m\right)\)
Do \(BC||DE\) (cùng vuông góc mặt đất AD)
Áp dụng định lý Thales:
\(\dfrac{AB}{AD}=\dfrac{BC}{DE}\Rightarrow\dfrac{0,8}{0,8+15}=\dfrac{2}{DE}\)
\(\Rightarrow DE=\dfrac{2.15,8}{0.8}=39,5\left(m\right)\)
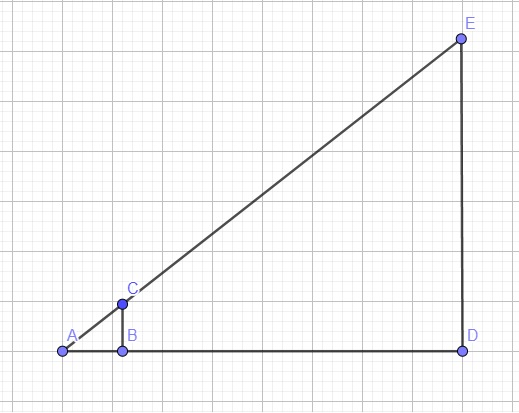
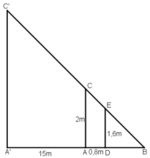
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB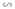 
ΔACB (vì DE // AC)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB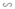 
ΔA’C’B (vì AC // A’C’)
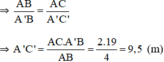
Vậy cây cao 9,5m.
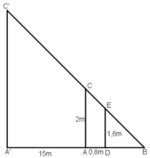
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB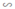 
ΔACB (vì DE // AC)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB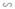 
ΔA’C’B (vì AC // A’C’)
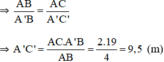
Vậy cây cao 9,5m.