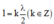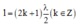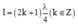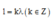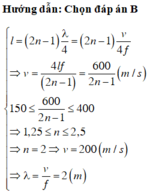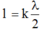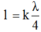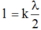Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tần số nhỏ nhất để tạo thành sóng dừng trong trường hợp 1 đầu cố định, 1 đầu tự do là trên dây có nửa bó sóng:
\(\ell=\dfrac{\lambda}{4}=\dfrac{v}{4f_0}\Rightarrow f_0=\dfrac{v}{4\ell}=4Hz\) (ứng với 1 nút sóng)
Các tần số xảy ra sóng dừng là số lẻ lần \(f_0\): \(f_n=(2n+1).4\), số nút sóng là lẻ thì n cũng là số lẻ.
\(\Rightarrow n=2k+1\)
\(\Rightarrow f =[2.(2k+1)+1].4=(4k+3).4\)
Ta có: \(19\le(4k+3).4\le 80\Rightarrow 0,43\le k\le 4,25\)
Vậy các giá trí k thỏa mãn là: 1; 2; 3; 4
Do vậy, có 4 lần xảy ra sóng dừng.
\(f=\frac{\left(k+\frac{1}{2}\right)\upsilon}{2l}\)
Số lẻ thì không phải chẵn
\(19\le f=8\left(k+\frac{1}{2}\right)\le80\rightarrow k=2,4,6,8\)
Vậy có 4 lần

Chọn D
+ Điều kiện có sóng dừng trên dây với một đầu cố định và một đầu tự do
 .
.

Chọn D
Trên dây chỉ có 1 nút sóng không kể đầu cố định
→ l = λ 2 + λ 4 → λ = 4 3 l > l

Đáp án D
+ Điều kiện để có sóng dừng trên dây với hai đầu cố định L = n λ 2 với n là số bó sóng.
Trên dây có 1 bụng sóng