Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Dao động tổng hợp x = x1 + x2
+ Khi x2 = 0 thì x1 = x - x2 = \(-5\sqrt{3}\)
+ Khi x1 = - 5 thì x2 = x - x1 = -2 + 5 = 3
Giả sử pt \(x_1=10\cos\left(\omega t\right)\) thì \(x_2=A_2\cos\left(\omega t+\varphi\right)\) (với \(\left|\varphi\right|<\frac{\pi}{2}\))
Theo giả thiết ta có:
\(\begin{cases}10\cos\left(\omega t\right)=-5\sqrt{3}\\A_2\cos\left(\omega t+\varphi\right)=0\end{cases}\)\(\Rightarrow\begin{cases}\cos\left(\omega t\right)=-\frac{\sqrt{3}}{2}\\\cos\left(\omega t+\varphi\right)=0\end{cases}\)
cos O M1 M2 -√3/2 60°
Do \(\left|\varphi\right|<\frac{\pi}{2}\) nên ta chỉ có trường hợp như hình trên thỏa mãn, nghĩa là ta tìm đc \(\varphi=-\frac{\pi}{3}\)
Mặt khác: \(\begin{cases}10\cos\left(\omega t'\right)=-5\\A_2\cos\left(\omega t'+\varphi\right)=3\end{cases}\)\(\Rightarrow\begin{cases}\cos\left(\omega t'\right)=-\frac{1}{2}\\\cos\left(\omega t'+\varphi\right)=\frac{3}{A_2}\end{cases}\)
Cũng biểu diễn trên đường tròn lượng giác như trên, ta được
cos O M1 M2 -1/2 1/2
\(\Rightarrow A_2=6cm\)
Biên độ tổng hợp:
\(A^2=10^2+6^2+2.10.6.\cos\frac{\pi}{3}\Rightarrow A=14\)cm.
Đáp án B
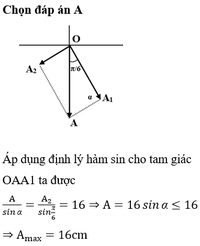
Định lý hàm sinh trong Δ O A A 1
A sin α = A 1 sin β = A 2 sin π 6 ⇒ A = A 2 sin π 6 sin α = 8 sin α
a = − ω 2 A vì vậy gia tốc muốn đạt giá trị cực đại khi Q đạt giá trị cực đại ⇒ A max = 8 c m = 0 , 08 m
Vậy a max = ω 2 A max = 10 2 .0 , 08 = 8 m / s
Đáp án D.
Ta có:
= 8cm
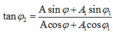
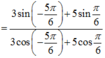
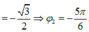
Phương trình của dao động thứ hai là:
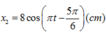
Nhận xét:
Có thể giải nhanh bài tập trên bằng cách sử dụng máy tính Casio fx-570 như sau:
Kết quả trên màn hình máy tính: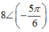 
và phương trình là
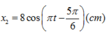
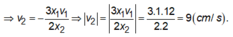
Đáp án C
Đạo hàm 2 vế ta được :
Thay vào phương trình (*) ta giải ra được :