




Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.








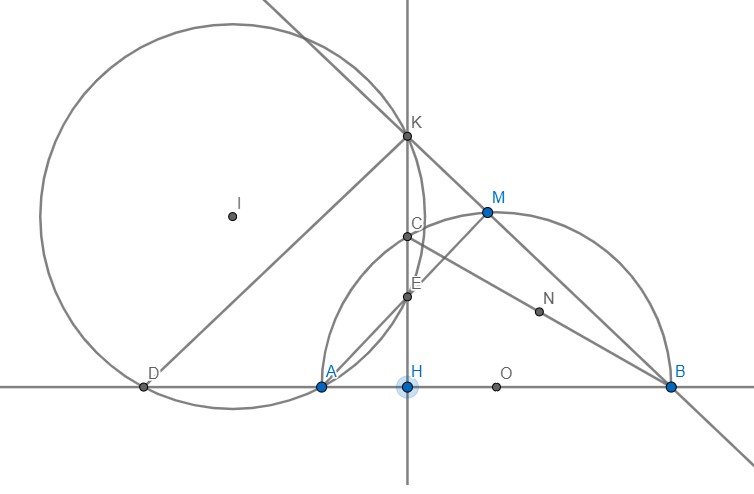
a) Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle ACD=\angle AMD=90\)
\(\Rightarrow ACMD\) nội tiếp
b) Ta có: \(\angle KCB+\angle KMB=90+90=180\Rightarrow KCBM\) nội tiếp
\(\Rightarrow\angle AKC=\angle MBA\)
Ta có: \(\angle NMK=\angle MBA=\angle AKC=\angle MKN\)
\(\Rightarrow\Delta NMK\) cân tại N
c) Vì B và E đối xứng với nhau qua C \(\Rightarrow\) CD là trung trực BE
\(\Rightarrow\angle DEC=\angle DBC=\angle AKC\Rightarrow AKDE\) nội tiếp

Xét △AKC và △DBC có: C = 900, góc KAC = góc CDB (cùng phụ với góc B) => △AKC đồng dạng với △DBC => AC/DC = KC/BC=> KC.DC = AC.BC (✳)
Cũng có △IAB vuông tại I có IC vuông góc với AB nên theo hệ thức lượng trong tam giác vuông ta có IC2=AC.CB (**)
Từ (*) và (**) => KC.DC=IC2 => KC/IC=IC/DC=1/2 => DC = 2IC
IC2=AC.BC=1/2R . 3/2R = 3/4R2 =>IC = \(\sqrt{ }\)3/2 R=> DC = căn 3 R.
S△ADB = 1/2 DC.AB=căn 3 R2

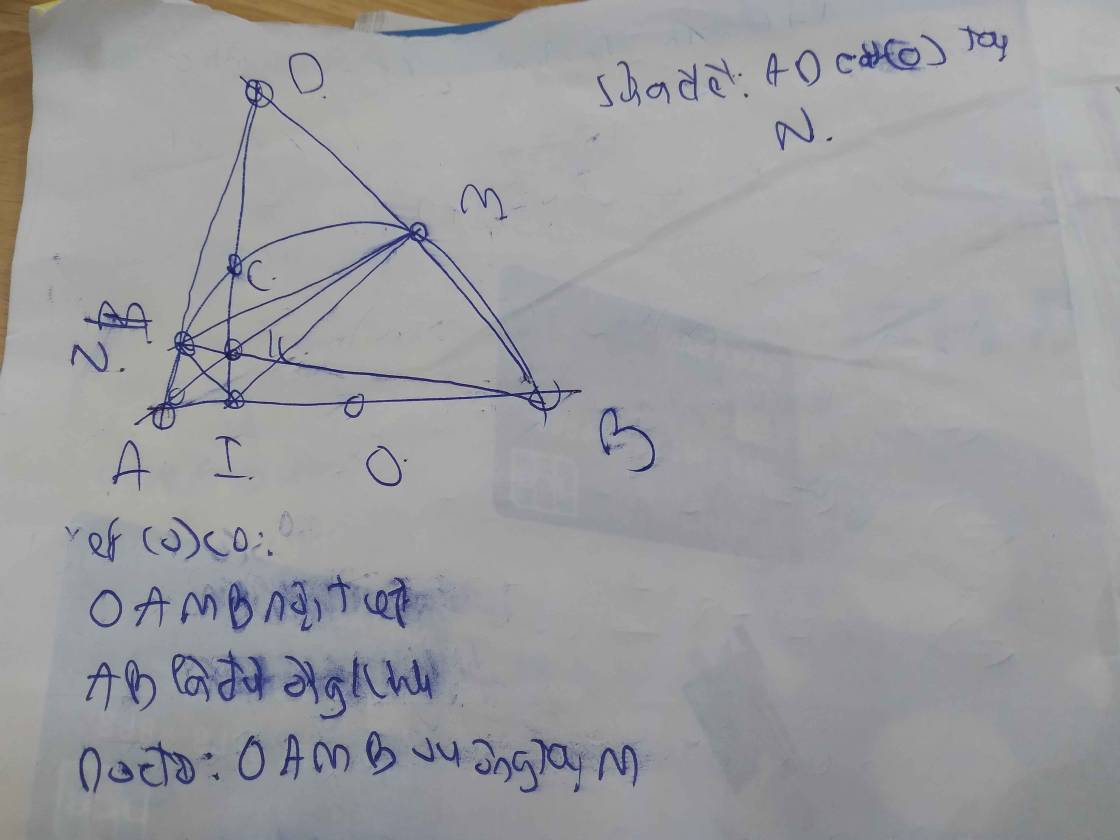
B C O A D d M K E N I H F P d'
1) Xét nửa đường tròn (O) đường kính BC có điểm N thuộc (O) => ^CNB = 900
=> ^CNE = 1800 - ^CNB = 900. Xét tứ giác CDNE có:
^CDE = ^CNE = 900 => Tứ giác CDNE nội tiếp đường tròn (đpcm).
2) Ta có điểm M thuộc nửa đường tròn (O) đường kính BC => ^CMB = 900
=> BM vuông góc CE. Xét \(\Delta\)BEC:
BM vuông góc CE; ED vuông góc BC; BM giao ED tại K => K là trực tâm \(\Delta\)BEC
=> CK vuông góc BE. Mà CN vuông góc BE (Do ^CNB = 900) => 3 điểm C;K;N thẳng hàng (đpcm).
3) Gọi giao điểm của MN với DE là H. Lấy F là trung điểm của EH. BH cắt CF tại điểm P.
Xét tứ giác CMHD: ^CMH = ^CDH = 900 => CMKD nội tiếp đường tròn => ^MCK = ^MDK (1)
Tương tự: ^NBK = ^NDK (2)
Từ (1) & (2) => ^MDK = ^NDK hay ^MDH = ^FDN
Tương tự: ^DMB = ^NMB => ^DMH = 2.^DMB (3)
Dễ thấy tứ giác BDME nội tiếp đường tròn => ^DMB = ^BED (2 góc nt chắn cung BD)
Hay ^DMB = ^NEF. Xét \(\Delta\)ENH vuông tại N: H là trung điểm EH
=> \(\Delta\)NEF cân tại F. Do ^DFN là góc ngoài \(\Delta\)NEF => ^DFN = 2.^NEF
Mà ^DMB = ^NEF (cmt) => ^DFN = 2.^DMB (4)
Từ (3) & (4) => ^DMH = ^DFN. Xét \(\Delta\)DMH và \(\Delta\)DFN:
^DMH = ^DFN ; ^MDH = ^FDN (cmt) => \(\Delta\)DMH ~ \(\Delta\)DFN (g.g)
=> \(\frac{DM}{DF}=\frac{DH}{DN}\)=> \(DH.DF=DM.DN\)(5)
Dễ chứng minh \(\Delta\)CMD ~ \(\Delta\)NBD => \(\frac{DM}{DB}=\frac{DC}{DN}\Rightarrow DM.DN=DB.DC\)(6)
Từ (5) & (6) => \(DH.DF=DB.DC\)\(\Rightarrow\frac{DH}{DB}=\frac{DC}{DF}\)
\(\Rightarrow\Delta\)CDH ~ \(\Delta\)FDB (c.g.c) => ^DHC = ^DBF. Mà ^DHC + ^DCH = 900
=> ^DBF + ^DCH = 900 => CH vuông góc BF.
Xét \(\Delta\)CFB: FD vuông góc BC; CH vuôn góc BF; H thuộc FD => H là trực tâm \(\Delta\)CFB
=> BH vuông góc CF (tại P). Ta có nửa đg trong (O) đg kính BC và có ^CPB = 900
=> P thuộc nửa đường tròn (O) => Tứ giác CMPB nội tiếp (O)
=> ^BMP = ^BCP (2 góc nt chắn cung BP) Hay ^HMP = ^DCP
Xét tứ giác CPHD: ^CPH = ^CDH = 900 => ^DCP + ^DHP = 1800
=> ^HMP + ^DHP = 1800 hay ^HMP + ^KHP = 1800 => Tứ giác MPHK nội tiếp đg tròn
=> ^KMH = ^KPH (2 góc nt chắn cung KH) hay ^KMN = ^KPB.
Lại có tứ giác EMKN nội tiếp đg tròn => ^KMN = ^KEN => ^KMN = ^KEB
=> ^KPB = ^KEB => Tứ giác BKPE nội tiếp đg tròn. Mà 3 điểm B;K;E cùng thuộc (I)
=> Điểm P cũng thuộc đg tròn (I) => IP=IB => I thuộc trung trực của BP
Mặt khác: OP=OB => O cũng thuộc trung trực của BP => OI là trung trực của BP
=> OI vuông góc BP. Mà CF vuông góc BP (cmt) => OI // CF (7)
I nằm trên trung trực của EK và F là trung điểm EK => IF vuông góc EK => IF vuông góc d
OC vuông góc d => OC // IF (8)
Từ (7) & (8) => Tứ giác COIF là hình bình hành => IF = OC = R (bk của (O))
=> Độ dài của IF không đổi. Mà IF là khoảng cách từ I đến d (Do IF vuông góc d)
=> I nằm trên đường thẳng d' // d và cách d một khoảng bằng bán kính của nửa đường tròn (O)
Vậy điểm I luôn nằm trên d' cố định song song với d và cách d 1 khoảng = bk nửa đg tròn (O) khi M thay đổi.

a) Xét (O) có
ΔAMB nội tiếp đường tròn(A,M,B\(\in\)(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
\(\Leftrightarrow AM\perp MB\) tại M
\(\Leftrightarrow AM\perp BD\) tại M
\(\Leftrightarrow\widehat{AMD}=90^0\)
Xét tứ giác ADMC có
\(\widehat{AMD}=\widehat{ACD}\left(=90^0\right)\)
\(\widehat{AMD}\) và \(\widehat{ACD}\) là hai góc cùng nhìn cạnh AD
Do đó: ADMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

AB cắt đường tròn ngoại tiếp tam giác AEK tại D
Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle EMB+\angle EHB=90+90=180\)
\(\Rightarrow EMBH\) nội tiếp \(\Rightarrow\angle KBD=\angle MBH=\angle AEH\)
Vì KEAD nội tiếp \(\Rightarrow\angle AEH=\angle KDB\Rightarrow\angle KBD=\angle KDB\)
\(\Rightarrow\Delta KDB\) cân tại K có KH là đường cao
\(\Rightarrow H\) là trung điểm BD mà B,H cố định \(\Rightarrow D\) cố định
Vì KEAD nội tiếp \(\Rightarrow I\in\) trung trực AD mà A,D cố định
\(\Rightarrow\) đpcm