Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GT ∆ABC cân tại A, AH BC
KL AHB = AHC
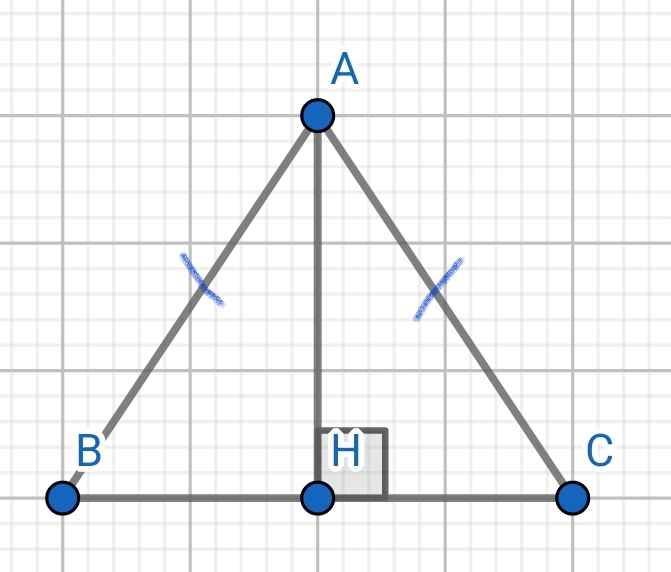
Xét hai tam giác vuông: ∆AHB và ∆AHC có:
AH chung
AB = AC (∆ABC cân tại A)
⇒ ∆AHB = ∆AHC (cạnh huyền - cạnh góc vuông)

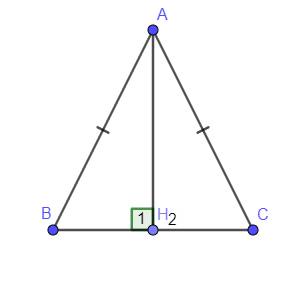
Có `AH⊥BC(GT)=>hat(H_1)=hat(H_2)(=90^0`
`Delta ABC` cân tại `A=>AB=AC`
Xét `Delta AHB` và `Delta AHC` có :
`{:(hat(H_1)=hat(H_2)(=90^0)),(AB=AC(cmt)),(AH-chung):}}`
`=>Delta AHB=Delta AHC(ch-cgv)(đpcm)`

GT: \(\Delta ABC\) nhọn
\(\Delta ABD\)vuông cân tại A
\(\Delta ACE\)vuông cân tại A
\(ÀH\perp BC\), \(AH\)cắt \(DE\)tại M
KL: a) \(\Delta ABD=\Delta ACD\)
b) \(DC\perp BE\)
c) M trung điểm DE

vì dùng máy tính nên ko vẽ hình đc thông cảm !!
a) giả thiết
Δ ABC cân tại A
AK là tia đối của AB
BK=BC
KH⊥BC(H∈BC)
KH cắt AC tại E
Kết luận
KH=AC
BE là tia phân giác của góc ABC
b) xét tam giác BAC và tam giác BHK có
\(\widehat{B} \) Chung
KH=BC (gt)
\(\widehat{BAC}=\widehat{BHK}=90\) (gt)
tam giác BAC = tam giác BHK (ch-gn)
=>KH=AC(2 góc tương ứng )
b)Xét Δ KBC có BK=BC(gt)
=> tam giác KBC cân tại B
Mà KH⊥BC=> KH là đường cao
AC⊥AB =>AC⊥KB(K∈AB)=>AC là đường cao
Mà AC giao vs KH tại E
=> E là trực tâm của tam giác
=> BE là đường cao (tc 3 đg cao trong tam giác)
=> BE là giân giác của góc \(\widehat{KBC}\)
=>BE là giân giác của góc \(\widehat{ABC} \) (A∈BK)

a) Xét 2 tam giác vuông: AMB và AMC có:
AM: cạnh chung
AB = AC (gt)
suy ra: tam giác AMB = tam giác AMC (ch-cgv)
b) Tam giác AMB = tam giácAMC
suy ra: góc BAM = góc CAM
Xét 2 tam giác vuông: AMH và AMK có:
AM: chung
góc HAM = góc
suy ra tam giác AMH = tam giác AMK
suy ra AH = AK
khỏi ghi kết luận giả thuyết thôi đc rồi =)))
GT:
△ABC cân tại A
AH ⊥ BC tại H
Làm gì có KL?